What Is Lcm Of 12 And 15
catanddoghelp
Nov 28, 2025 · 14 min read
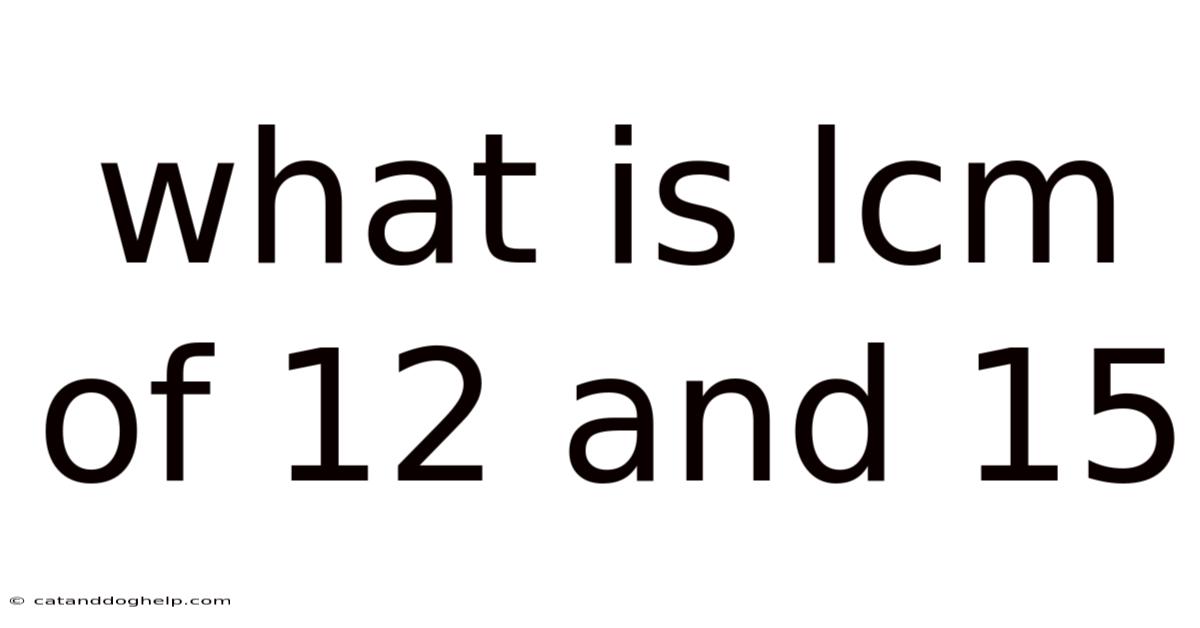
Table of Contents
Imagine you are organizing a party and want to buy both cupcakes, which come in packs of 12, and juice boxes, which come in packs of 15. To ensure that you have the same number of cupcakes and juice boxes without having any leftovers, you need to figure out the smallest number of each to buy. This is where the concept of the least common multiple, or LCM, comes into play. Finding the LCM of 12 and 15 helps you determine that magic number, allowing you to perfectly balance your party supplies.
The least common multiple is a fundamental concept in mathematics that plays a crucial role in various real-life scenarios, from scheduling events to dividing quantities evenly. Whether you're a student grappling with fractions or a professional dealing with logistical puzzles, understanding how to calculate the LCM can greatly simplify your tasks. In this article, we’ll explore what exactly the LCM is, how to find the LCM of 12 and 15, and why this concept is so useful in everyday life. Let's dive in!
Main Subheading
The least common multiple, or LCM, is the smallest positive integer that is perfectly divisible by two or more numbers. This concept is foundational in number theory and has practical applications across various fields. To fully grasp the LCM, it's helpful to first understand its relationship to multiples and common multiples. A multiple of a number is the result of multiplying that number by an integer. For instance, the multiples of 12 are 12, 24, 36, 48, and so on, while the multiples of 15 are 15, 30, 45, 60, and so on.
When comparing the multiples of two or more numbers, any multiple that appears in both lists is a common multiple. For example, common multiples of 12 and 15 include 60, 120, and 180. Among these common multiples, the smallest is the least common multiple. Therefore, the LCM of 12 and 15 is the smallest number that both 12 and 15 can divide into evenly. This concept isn't just a theoretical exercise; it has practical implications in many real-world situations, such as simplifying fractions, scheduling events, and solving algebraic problems.
Comprehensive Overview
The concept of the least common multiple (LCM) is steeped in mathematical history and is closely tied to the development of number theory. While it is difficult to pinpoint the exact origins of the LCM, its principles have been used since ancient times in various mathematical calculations and problem-solving scenarios. Ancient civilizations, including the Egyptians and Babylonians, used similar concepts in their calculations related to fractions and proportions.
Definitions and Scientific Foundations
At its core, the LCM is a foundational concept in arithmetic and number theory. Here are some key definitions to clarify its meaning:
- Multiple: A multiple of a number is the product of that number and any integer. For example, multiples of 5 are 5, 10, 15, 20, and so on.
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of each of those numbers. For instance, a common multiple of 4 and 6 is 12 because 12 is a multiple of both 4 and 6.
- Least Common Multiple (LCM): The smallest positive integer that is a common multiple of two or more numbers. It's the smallest number that each of the given numbers can divide into without leaving a remainder.
The LCM is closely related to the greatest common divisor (GCD), also known as the highest common factor (HCF). The GCD of two numbers is the largest positive integer that divides both numbers without any remainder. The relationship between the LCM and GCD can be expressed by the formula:
LCM (a, b) = |a * b| / GCD(a, b)
This formula highlights that the LCM and GCD are inversely related. Knowing the GCD of two numbers can simplify the calculation of their LCM, and vice versa.
Methods to Find the LCM
There are several methods to find the LCM of two or more numbers, each with its advantages depending on the specific numbers involved. Here are three common methods:
- Listing Multiples:
- List the multiples of each number until you find a common multiple.
- Identify the smallest common multiple.
- For example, to find the LCM of 12 and 15:
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, ...
- The LCM of 12 and 15 is 60.
- Prime Factorization:
- Find the prime factorization of each number.
- Identify all unique prime factors and their highest powers present in any of the factorizations.
- Multiply these highest powers together to get the LCM.
- For example, to find the LCM of 12 and 15:
- Prime factorization of 12: 2^2 * 3
- Prime factorization of 15: 3 * 5
- The highest powers of each prime factor are: 2^2, 3, and 5.
- LCM = 2^2 * 3 * 5 = 4 * 3 * 5 = 60.
- Using the GCD:
- Find the greatest common divisor (GCD) of the two numbers.
- Use the formula: LCM (a, b) = |a * b| / GCD(a, b)
- For example, to find the LCM of 12 and 15:
- The GCD of 12 and 15 is 3.
- LCM = (12 * 15) / 3 = 180 / 3 = 60.
Practical Applications of LCM
The LCM is not just a theoretical concept; it has several practical applications in various fields:
- Mathematics: Simplifying fractions (finding a common denominator), solving algebraic equations, and understanding number patterns.
- Scheduling: Coordinating events or tasks that occur at different intervals. For example, if one task occurs every 12 days and another every 15 days, the LCM (60) tells you when both tasks will occur on the same day again.
- Engineering: Designing systems that require synchronized or periodic actions.
- Computer Science: Optimizing algorithms and data structures.
- Everyday Life: Planning events, dividing quantities equally, and understanding time-related problems.
Examples of Finding LCM in Real-World Scenarios
Consider these examples to illustrate the real-world applicability of the LCM:
- Synchronizing Alarms: Suppose you have two alarms, one set to ring every 12 minutes and another set to ring every 15 minutes. When will both alarms ring together? The LCM of 12 and 15 is 60, so both alarms will ring together every 60 minutes.
- Arranging Tiles: You want to tile a rectangular area with square tiles. If the area is 12 inches wide and 15 inches long, what is the smallest square tile you can use without cutting any tiles? The LCM of 12 and 15 is 60, which means you can create a pattern where the dimensions repeat every 60 inches. However, this doesn't directly answer the question about the smallest square tile. To find the largest square tile that fits evenly, you need the GCD, which is 3.
- Cooking and Baking: Adjusting recipes that serve different numbers of people. Understanding the LCM helps in scaling ingredients proportionately.
Benefits of Understanding LCM
Having a solid understanding of the LCM offers numerous benefits:
- Problem-Solving: Simplifies complex problems by finding common ground between different quantities.
- Efficiency: Allows for efficient planning and scheduling in various scenarios.
- Accuracy: Ensures precise calculations in mathematical and practical applications.
- Versatility: Applicable in a wide range of fields, from mathematics and engineering to everyday life.
Trends and Latest Developments
While the fundamental concept of the least common multiple (LCM) remains constant, its application and the methods used to calculate it have evolved with technological advancements. Today, calculators and computer software can quickly compute the LCM of large numbers, making it easier than ever to solve complex problems.
Computational Tools
The advent of computers and sophisticated calculators has significantly streamlined the process of finding the LCM. Online calculators and software tools can instantly compute the LCM of multiple numbers, regardless of their size. This capability is particularly useful in fields like cryptography and large-scale data analysis, where dealing with very large numbers is common.
Algorithmic Optimizations
In computer science, optimizing algorithms often involves finding efficient ways to compute the LCM. Researchers have developed algorithms that reduce the computational complexity of finding the LCM, making it faster and more efficient, especially for large datasets. These algorithms are used in various applications, including scheduling tasks in operating systems and optimizing database queries.
Educational Approaches
Modern educational approaches emphasize understanding the conceptual basis of the LCM rather than rote memorization. Interactive tools, visual aids, and real-world examples are used to help students grasp the significance of the LCM and its practical applications. This shift towards conceptual understanding aims to make mathematics more accessible and relevant for students.
Interdisciplinary Applications
The LCM continues to find new applications in interdisciplinary fields. For example, in logistics and supply chain management, the LCM is used to optimize delivery schedules and synchronize various processes. In finance, it can be used to analyze investment cycles and plan financial strategies.
Data Analysis and LCM
With the rise of big data, the LCM is used in data analysis to identify patterns and cycles. By analyzing large datasets, analysts can use the LCM to find common intervals or periods in the data, which can provide valuable insights for decision-making.
Professional Insights
From a professional standpoint, understanding the LCM can enhance problem-solving skills and improve decision-making. Whether you are an engineer, a financial analyst, or a project manager, the ability to find and apply the LCM can help you optimize processes, manage resources effectively, and achieve better outcomes.
Tips and Expert Advice
Finding the least common multiple (LCM) can be straightforward with the right strategies. Here are some practical tips and expert advice to help you master this concept:
1. Understand the Basics Thoroughly
Ensure you have a solid grasp of multiples, common multiples, and prime factorization. Knowing these fundamentals will make finding the LCM much easier.
- Why it matters: A clear understanding of these basics provides a strong foundation for more complex calculations.
- How to implement: Practice identifying multiples of different numbers and breaking down numbers into their prime factors.
2. Choose the Right Method
The best method for finding the LCM depends on the numbers involved. For small numbers, listing multiples might be the easiest approach. For larger numbers, prime factorization or using the GCD is more efficient.
- Why it matters: Selecting the appropriate method saves time and reduces the risk of errors.
- How to implement: Assess the numbers you are working with and choose the method that best suits them. For instance, when finding the LCM of 12 and 15, listing multiples or using prime factorization works well.
3. Use Prime Factorization for Accuracy
Prime factorization is a reliable method for finding the LCM, especially for larger numbers. Breaking down each number into its prime factors ensures you account for all necessary factors.
- Why it matters: Prime factorization guarantees accuracy and helps avoid overlooking factors.
- How to implement: Practice breaking down numbers into their prime factors and systematically identify the highest powers of each prime factor.
4. Simplify with the GCD
If you know the greatest common divisor (GCD) of the numbers, you can easily find the LCM using the formula: LCM (a, b) = |a * b| / GCD(a, b).
- Why it matters: Using the GCD simplifies the calculation and provides an alternative approach.
- How to implement: Learn how to find the GCD using methods like the Euclidean algorithm and apply the formula to calculate the LCM.
5. Practice Regularly
Like any mathematical skill, mastering the LCM requires practice. Work through various examples and problems to build your proficiency.
- Why it matters: Regular practice reinforces your understanding and improves your speed and accuracy.
- How to implement: Set aside time to practice finding the LCM of different sets of numbers. Use online resources, textbooks, and worksheets to find practice problems.
6. Apply LCM in Real-World Scenarios
Understanding how the LCM applies to real-world situations can make the concept more relatable and easier to remember. Look for opportunities to use the LCM in everyday tasks and problems.
- Why it matters: Real-world applications demonstrate the practical value of the LCM and enhance your understanding.
- How to implement: Apply the LCM to problems involving scheduling, dividing quantities, or synchronizing events.
7. Use Online Tools and Calculators
Leverage online LCM calculators and tools to check your work and gain a better understanding of the process. These tools can quickly compute the LCM and show you the steps involved.
- Why it matters: Online tools provide immediate feedback and help you identify errors.
- How to implement: Use online LCM calculators to verify your calculations and explore different examples.
8. Break Down Complex Problems
If you encounter a complex problem involving the LCM, break it down into smaller, more manageable steps. This approach can make the problem less intimidating and easier to solve.
- Why it matters: Breaking down complex problems simplifies the process and reduces the risk of errors.
- How to implement: Divide the problem into smaller parts and solve each part individually before combining the results.
9. Seek Help When Needed
Don't hesitate to seek help from teachers, tutors, or online resources if you are struggling with the LCM. Getting clarification from others can help you overcome difficulties and improve your understanding.
- Why it matters: Seeking help ensures you don't get stuck on challenging concepts and allows you to learn from others.
- How to implement: Reach out to teachers, tutors, or online forums for assistance and ask specific questions about the areas you are struggling with.
FAQ
Q: What is the least common multiple (LCM)?
A: The least common multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. In simpler terms, it's the smallest number that each of the given numbers can divide into evenly.
Q: Why is the LCM important?
A: The LCM is important because it simplifies various mathematical problems, such as adding and subtracting fractions with different denominators. It also has practical applications in scheduling, engineering, and everyday life, such as planning events or dividing quantities equally.
Q: How do you find the LCM of two numbers?
A: There are several methods to find the LCM of two numbers, including listing multiples, prime factorization, and using the greatest common divisor (GCD). Listing multiples involves writing out the multiples of each number until you find a common one. Prime factorization involves breaking down each number into its prime factors and then multiplying the highest powers of each factor. Using the GCD involves finding the GCD of the two numbers and then using the formula LCM (a, b) = |a * b| / GCD(a, b).
Q: What is the LCM of 12 and 15?
A: The LCM of 12 and 15 is 60.
Q: Can the LCM be larger than the numbers you are finding it for?
A: Yes, the LCM is usually larger than the numbers you are finding it for, unless the numbers are multiples of each other. For example, the LCM of 4 and 8 is 8, but the LCM of 4 and 6 is 12, which is larger than both 4 and 6.
Q: Is the LCM the same as the greatest common divisor (GCD)?
A: No, the LCM and GCD are different concepts. The LCM is the smallest multiple that two or more numbers share, while the GCD is the largest factor that two or more numbers share. They are related by the formula LCM (a, b) = |a * b| / GCD(a, b).
Q: How is the LCM used in real life?
A: The LCM is used in various real-life scenarios, such as:
- Scheduling: Coordinating events that occur at different intervals.
- Cooking: Adjusting recipes that serve different numbers of people.
- Construction: Planning the layout of tiles or bricks.
- Finance: Analyzing investment cycles.
Q: What if I need to find the LCM of more than two numbers?
A: The same methods used to find the LCM of two numbers can be extended to more than two numbers. For example, you can use prime factorization to find the prime factors of all the numbers and then multiply the highest powers of each factor.
Conclusion
Understanding the least common multiple (LCM) is essential for anyone looking to enhance their mathematical toolkit and tackle real-world problems more effectively. By grasping the fundamentals, exploring different calculation methods, and recognizing the practical applications, you can confidently apply this concept in various scenarios. Whether you're a student, a professional, or simply someone who enjoys problem-solving, mastering the LCM will undoubtedly prove beneficial.
Now that you have a comprehensive understanding of the LCM, take the next step and apply your knowledge. Try solving LCM problems, explore real-world applications, and share your insights with others. Engage in discussions, ask questions, and continue to deepen your understanding. By actively using your newfound knowledge, you can reinforce your learning and unlock the full potential of the least common multiple.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 8 And 2
Nov 28, 2025
-
Difference Between Prime And Composite Numbers
Nov 28, 2025
-
What Is A Secant In A Circle
Nov 28, 2025
-
What Is Lcm Of 12 And 15
Nov 28, 2025
-
What Are The Factors Of 55
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.