332 In Base 4 To Base 10
catanddoghelp
Nov 21, 2025 · 9 min read
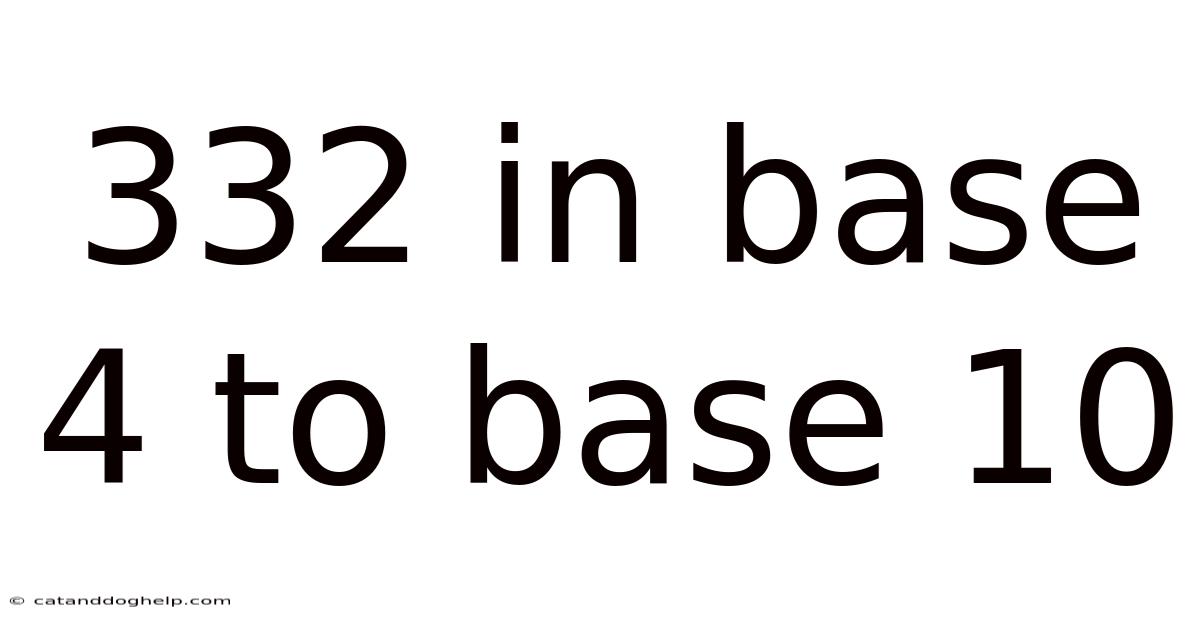
Table of Contents
Imagine you're explaining numbers to a curious child. You use colorful blocks, each representing a different value. In our everyday world, we use a system where each block can represent ten values (0-9), which we call base 10. But what if we only had four colors of blocks (0-3)? That's base 4, and understanding how to convert numbers between these systems opens up a whole new way of thinking about how we represent quantities.
The number 332 in base 4 looks deceptively similar to a familiar base 10 number, but its value is entirely different. It’s crucial to understand the underlying principles of positional notation to correctly decipher its true worth in our commonly used base 10 system. This article will meticulously guide you through the process of converting 332 (base 4) to base 10, providing a solid understanding of number base conversions along the way.
Understanding Base 4 and Base 10
Base 4, also known as the quaternary numeral system, is a positional numeral system using 4 as its base. This means that only four symbols are used to represent all numbers: 0, 1, 2, and 3. Each position in a base 4 number represents a power of 4. Just like in the decimal system (base 10) where each position represents a power of 10 (ones, tens, hundreds, etc.), in base 4, each position represents powers of 4 (ones, fours, sixteens, etc.).
Base 10, the decimal system, is the number system we use every day. It uses ten digits (0-9) to represent numbers, with each position representing a power of 10. Understanding the place value system is key to grasping number conversions. For example, in the number 345, the 3 represents 3 hundreds (3 x 10^2), the 4 represents 4 tens (4 x 10^1), and the 5 represents 5 ones (5 x 10^0).
The Foundation of Number Systems
At its core, a number system is a way to represent quantities using symbols. The radix, or base, of a number system defines the number of unique digits used to represent numbers. In base 10, the radix is 10, and we use digits 0 through 9. Similarly, in base 4, the radix is 4, and we use digits 0 through 3.
The positional notation system is fundamental to how we represent numbers in both base 4 and base 10. The value of a digit depends on its position within the number. Each position corresponds to a power of the base. Starting from the rightmost digit, the positions represent base^0, base^1, base^2, and so on. For instance, in base 10, the number 123 is (1 x 10^2) + (2 x 10^1) + (3 x 10^0). This concept applies equally to base 4.
Historically, different cultures have used various number systems. The Babylonians used a base 60 system, which influences our modern measurement of time (60 seconds in a minute, 60 minutes in an hour). The Mayans used a base 20 system. The prevalence of base 10 likely stems from the fact that humans have ten fingers, making it a natural choice for counting. Regardless of the base, the underlying principles of positional notation remain constant.
Understanding different number systems is not merely an academic exercise. It's critical in computer science, where binary (base 2) is fundamental. Computers use bits (binary digits) to represent all data and instructions. Converting between different number systems allows us to understand how computers process information. Furthermore, in cryptography and data encoding, understanding number systems is vital for secure communication and data storage.
Converting between bases helps develop a deeper understanding of numerical representation. It reinforces the idea that a number's value is independent of the base in which it is expressed. For example, the quantity "ten" can be represented as 10 in base 10, 1010 in base 2, or 22 in base 4. The underlying quantity remains the same, only the representation changes.
Converting 332 (base 4) to Base 10: A Step-by-Step Guide
To convert the number 332 from base 4 to base 10, we need to understand the positional values in base 4. Starting from the right, the positions represent:
- 4^0 = 1 (the ones place)
- 4^1 = 4 (the fours place)
- 4^2 = 16 (the sixteens place)
Therefore, the base 4 number 332 can be broken down as follows:
(3 x 4^2) + (3 x 4^1) + (2 x 4^0)
Now, let's calculate each part:
- 3 x 4^2 = 3 x 16 = 48
- 3 x 4^1 = 3 x 4 = 12
- 2 x 4^0 = 2 x 1 = 2
Finally, we add these values together:
48 + 12 + 2 = 62
So, 332 in base 4 is equal to 62 in base 10.
Current Trends and Developments in Number Systems
While base 10 remains the standard for everyday use, other number systems are crucial in specific fields. In computer science, binary (base 2), octal (base 8), and hexadecimal (base 16) are widely used. These bases are convenient for representing binary data in a more human-readable format. For example, hexadecimal is often used to represent memory addresses and color codes.
There's ongoing research into more efficient and specialized number systems for specific applications. For example, balanced ternary (base 3 using digits -1, 0, and 1) has been explored for its potential advantages in certain computational tasks. Residue number systems are also researched for their parallel processing capabilities.
The rise of quantum computing is also influencing the development of new number representations. Qubits, the basic units of quantum information, can exist in a superposition of states, unlike classical bits which are either 0 or 1. This has led to investigations into quantum number systems that can leverage the unique properties of qubits.
From a pedagogical perspective, teaching different number systems helps students develop a deeper understanding of mathematical concepts. It reinforces the importance of place value, algebraic thinking, and problem-solving skills. Exposing students to different bases can make math more engaging and less abstract.
The internet and online calculators have made converting between number systems easier than ever. Numerous websites and apps provide tools for converting between various bases, making it accessible to anyone. This accessibility promotes broader understanding and experimentation with different numerical representations.
Practical Tips and Expert Advice for Base Conversions
When converting between bases, it's crucial to be organized and systematic. Here are some practical tips:
-
Understand Place Value: Always start by understanding the place values of each digit in the number system you are converting from. For example, in base 4, remember that the place values are powers of 4 (..., 4^3, 4^2, 4^1, 4^0).
-
Break It Down: Break down the number into its individual digits and their corresponding place values. This makes the conversion process less overwhelming.
-
Multiply and Add: Multiply each digit by its place value and then add up the results. This will give you the equivalent value in the target base.
-
Double-Check Your Work: Always double-check your calculations to avoid errors. A small mistake can lead to a completely incorrect result.
-
Use Online Tools: Utilize online base converters to verify your calculations and gain confidence in your understanding.
Here's an example applying these tips to converting 213 (base 4) to base 10:
- Understand Place Value: In base 4, the place values are 4^2, 4^1, and 4^0 (16, 4, and 1).
- Break It Down: 213 (base 4) = (2 x 4^2) + (1 x 4^1) + (3 x 4^0)
- Multiply and Add: (2 x 16) + (1 x 4) + (3 x 1) = 32 + 4 + 3 = 39
- Double-Check Your Work: Verify the calculation to ensure accuracy.
- Use Online Tools: Use a base converter to confirm that 213 (base 4) is indeed 39 (base 10).
When converting from base 10 to another base, the process involves repeated division. Here's how to convert 62 (base 10) to base 4:
- Divide 62 by 4: 62 ÷ 4 = 15 remainder 2
- Divide 15 by 4: 15 ÷ 4 = 3 remainder 3
- Divide 3 by 4: 3 ÷ 4 = 0 remainder 3
Read the remainders in reverse order: 332. So, 62 (base 10) is 332 (base 4).
Understanding the underlying math is more important than just memorizing steps. Focus on the why behind the process. Why do we multiply by powers of the base? Why do we read remainders in reverse order when converting from base 10? Answering these questions will solidify your understanding and make you a more confident converter.
Practice is essential. Start with simple examples and gradually work your way up to more complex conversions. The more you practice, the more comfortable and proficient you will become.
Frequently Asked Questions
Q: Why do we use different number systems?
A: Different number systems are used for different purposes. Base 10 is convenient for everyday human calculations. Binary (base 2) is fundamental to computers because it can be easily represented by electrical signals (on or off). Other bases like hexadecimal are used to represent binary data in a more compact and readable format.
Q: Is base 4 commonly used?
A: No, base 4 is not commonly used in everyday life. However, it has applications in some areas, such as representing quaternary code in computing and in some mathematical puzzles.
Q: Can any number be converted to any base?
A: Yes, any number can be converted to any base. The underlying quantity remains the same; only the representation changes.
Q: What happens if I have a digit larger than the base in my number?
A: If you encounter a digit larger than the base, it is not a valid number in that base. For example, 52 in base 4 is invalid because 5 is not a valid digit in base 4 (base 4 uses only 0, 1, 2, and 3).
Q: Are there any online tools to help with base conversions?
A: Yes, many online tools and calculators can perform base conversions. These tools can be helpful for checking your work and exploring different number systems.
Conclusion
Converting numbers between different bases, like understanding that 332 in base 4 is equivalent to 62 in base 10, may seem like an abstract exercise. However, it reinforces fundamental mathematical principles and broadens your understanding of how numbers are represented. It underscores the importance of positional notation and the role of the base in defining a number system.
Understanding different number systems is not just a theoretical concept. It has practical applications in computer science, cryptography, and other fields. By mastering base conversions, you gain a valuable skill that enhances your problem-solving abilities and deepens your appreciation for the elegance and versatility of mathematics.
Now that you've learned how to convert from base 4 to base 10, put your knowledge to the test! Try converting other base 4 numbers to base 10, or vice versa. Share your results and any questions you have in the comments below. Let's continue the learning journey together!
Latest Posts
Latest Posts
-
What Are The Factors Of 17
Nov 21, 2025
-
Difference Between A Rhombus And A Parallelogram
Nov 21, 2025
-
332 In Base 4 To Base 10
Nov 21, 2025
-
Lowest Common Multiple Of 4 And 7
Nov 21, 2025
-
Ray Diagram For A Concave Lens
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 332 In Base 4 To Base 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.