What Is The Percentage Of 0.5
catanddoghelp
Nov 28, 2025 · 10 min read
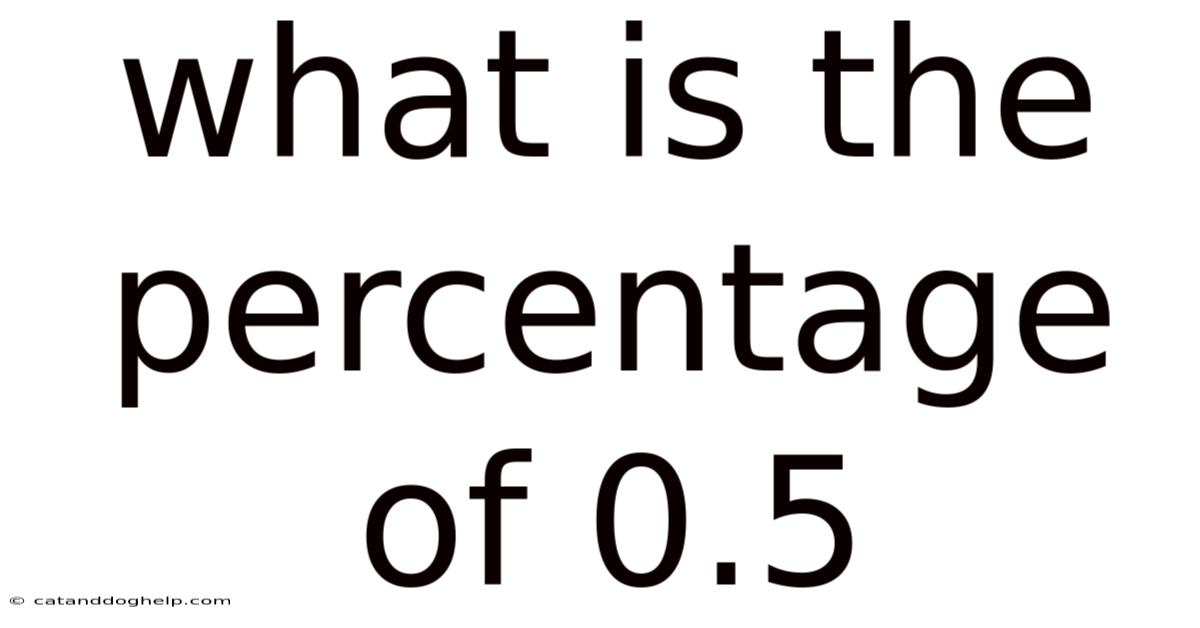
Table of Contents
Imagine you're baking a cake and the recipe calls for half a cup of sugar. You know that's 0.5 cups, but what if you needed to express that amount as a percentage? Or picture yourself getting a 0.5 raise at your job. It doesn't sound like much, but understanding how that translates into a percentage of your overall salary can be quite revealing.
The concept of percentages is woven into the fabric of our daily lives, from calculating discounts at the store to understanding statistics in the news. While we often deal with whole numbers when thinking about percentages, it's equally important to understand how decimals, like 0.5, fit into the picture. Converting 0.5 into a percentage is a fundamental skill that bridges the gap between decimals and the more relatable world of percentages, allowing us to grasp proportions and make informed decisions with greater confidence.
Understanding the Percentage of 0.5
Percentages are a fundamental concept in mathematics and are extensively used in everyday life. They provide a standardized way to express proportions, making it easier to compare different quantities and understand relative sizes. Converting a decimal like 0.5 into a percentage is a basic skill that allows us to translate decimal values into a more readily understandable format. The percentage of 0.5, specifically, serves as a straightforward example to illustrate the process of converting decimals to percentages, which is essential in various fields, from finance to statistics.
At its core, a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say "50 percent," we mean 50 out of every 100, which can be written as 50/100 or 0.5 in decimal form. Understanding this basic relationship is crucial for grasping how decimals and percentages are interconnected.
Decoding Percentages: Definitions and Foundations
A percentage is a ratio or number expressed as a fraction of 100. It's a dimensionless number, meaning it doesn't have any units associated with it. Percentages are used to express how large one quantity is relative to another quantity. The quantity being compared is usually considered as a whole, and the percentage represents a part of that whole.
The formula to convert a decimal to a percentage is quite simple:
Percentage = Decimal × 100
This formula is based on the idea that a percentage is a way of expressing a part of a whole, where the whole is considered to be 100. Multiplying a decimal by 100 effectively scales it to this "out of 100" scale, giving us the percentage.
The concept of percentages has its roots in ancient Rome. As early as the Roman Empire, emperors would often levy taxes expressed as fractions of assets. One such tax was the centesima rerum venalium, which was a 1/100 tax on goods sold at auction. This early form of percentage was used for financial calculations and resource management.
Over time, the use of percentages spread, particularly during the Middle Ages and the Renaissance. As trade and commerce grew, the need for a standardized way to express proportions became increasingly important. Italian merchants in the 15th century played a significant role in popularizing the use of percentages for calculating interest, profits, and taxes.
The symbol "%" for percentage evolved gradually. In the beginning, the term per cento was used, often abbreviated as "p. cento." Over time, this abbreviation was further shortened, and the symbol we recognize today emerged. By the 17th century, the "%" symbol was widely used in mathematical and financial texts.
Percentages are applied in a vast array of fields:
- Finance: Interest rates, investment returns, inflation rates, and budget allocations are all commonly expressed as percentages.
- Statistics: Percentages are used to describe data sets, calculate probabilities, and present survey results.
- Retail: Discounts, sales tax, and profit margins are often expressed as percentages.
- Science: Experimental results, error margins, and concentrations of solutions are frequently expressed as percentages.
- Education: Grades, test scores, and performance metrics are often presented as percentages.
Converting 0.5 to a percentage is straightforward using the formula mentioned earlier. Multiplying 0.5 by 100 gives us:
- 5 × 100 = 50
Therefore, 0.5 is equal to 50%. This means that 0.5 represents 50 out of every 100 parts, or half of the whole.
Understanding this conversion helps in various practical scenarios. For instance, if a store offers a 0.5 discount on an item, it means you are getting a 50% discount. Similarly, if a student scores 0.5 on a quiz graded out of 1, they have answered 50% of the questions correctly.
Trends and Latest Developments
The use of percentages remains ubiquitous in modern society, and there are several notable trends and developments in how they are applied and understood.
Data Visualization: With the explosion of data in various fields, there is an increasing emphasis on presenting percentages in visually appealing and easily understandable formats. Tools like charts, graphs, and infographics are used to communicate proportional data effectively. Software and platforms such as Tableau, Power BI, and Google Data Studio offer functionalities to dynamically display percentages and related data, enhancing data-driven decision-making.
Financial Literacy: There is a growing focus on improving financial literacy among the general population. Understanding percentages is crucial for making informed financial decisions, such as managing personal budgets, evaluating investment options, and understanding loan terms. Educational initiatives and online resources are increasingly emphasizing the importance of understanding percentages in personal finance.
Statistics and Research: In statistical analysis, percentages are extensively used for summarizing and interpreting data. Researchers often use percentages to present findings from surveys, experiments, and observational studies. The interpretation of percentages in research requires careful consideration of sample sizes, confidence intervals, and potential biases to avoid misrepresentation of the data.
Machine Learning: Percentages play a significant role in machine learning, particularly in evaluating model performance. Metrics such as accuracy, precision, and recall are often expressed as percentages to quantify the effectiveness of machine learning algorithms. These percentages help data scientists and machine learning engineers optimize models and make informed decisions about model deployment.
Consumer Behavior: Businesses use percentages extensively to analyze consumer behavior. Market share, customer satisfaction rates, and conversion rates are often expressed as percentages to track performance and identify areas for improvement. Understanding these percentages helps businesses tailor their marketing strategies, improve customer service, and optimize their product offerings.
Recent studies and surveys highlight the importance of understanding percentages in various contexts. For example, a study on financial literacy found that individuals with a better understanding of percentages are more likely to make sound financial decisions and avoid debt. Another survey on consumer behavior showed that consumers are more likely to be influenced by percentage discounts than by absolute dollar amounts, highlighting the psychological impact of percentages in marketing.
The rise of digital platforms and online tools has made it easier to calculate and interpret percentages. Online calculators, spreadsheet software, and data analysis tools provide functionalities to perform percentage calculations quickly and accurately. These tools are widely used in education, business, and personal finance, empowering individuals to work with percentages more effectively.
Tips and Expert Advice
Understanding and using percentages effectively can significantly enhance decision-making in various aspects of life. Here are some practical tips and expert advice to help you master the use of percentages:
Understand the Base: Always be clear about what the base or the whole is when dealing with percentages. The percentage represents a proportion of this base, so understanding what the base represents is crucial. For example, if a store offers a 20% discount, make sure you know what the original price (the base) is before calculating the actual discount amount.
Avoid Percentage of Percentage Confusion: Be careful when dealing with percentage increases or decreases. If a quantity increases by 10% and then decreases by 10%, it will not return to the original value. This is because the 10% decrease is calculated on the increased value, not the original value. For example, if an item costs $100 and increases by 10% to $110, a subsequent 10% decrease will be 10% of $110, which is $11, bringing the price down to $99, not $100.
Use Benchmarks: Develop a sense of what common percentages represent. For example, 25% is one-quarter, 50% is one-half, and 75% is three-quarters. This can help you quickly estimate and understand proportions without needing to perform exact calculations.
Double-Check Calculations: Especially in critical financial calculations, always double-check your percentage calculations to ensure accuracy. Small errors in percentage calculations can lead to significant discrepancies, particularly when dealing with large amounts of money or data.
Use Percentages for Comparison: Percentages are useful for comparing relative changes. For example, instead of comparing the absolute increase in sales between two products, compare the percentage increase to account for differences in initial sales volumes.
Be Aware of Context: The interpretation of percentages can depend on the context. For example, a 5% increase in sales may be significant for a large company but negligible for a small business. Always consider the relevant factors and benchmarks when interpreting percentages.
Learn to Estimate: Develop the skill to estimate percentages quickly in your head. This can be useful in everyday situations such as calculating tips, estimating discounts, or understanding statistics presented in the news. Rounding numbers to the nearest convenient value can make estimation easier.
Apply in Real-World Scenarios: Practice applying percentages in real-world scenarios to reinforce your understanding. For example, calculate the sales tax on a purchase, determine the tip amount at a restaurant, or analyze the performance of your investment portfolio.
By following these tips and advice, you can enhance your ability to work with percentages effectively and make more informed decisions in various aspects of your life.
FAQ:
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator to get the decimal equivalent, then multiply by 100. For example, to convert 1/4 to a percentage, divide 1 by 4 to get 0.25, and then multiply by 100 to get 25%.
Q: What is the difference between a percentage and a percentage point?
A: A percentage is a proportion of a whole, while a percentage point is the arithmetic difference between two percentages. For example, if a rate increases from 10% to 12%, it has increased by 2 percentage points, which is a 20% relative increase (2/10 = 0.2 or 20%).
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, use the formula: [(New Value - Original Value) / Original Value] × 100. For a percentage decrease, use the formula: [(Original Value - New Value) / Original Value] × 100.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This usually occurs when comparing a quantity to a smaller base. For example, if a company's revenue doubles, it has increased by 100%. If it triples, it has increased by 200%.
Q: How do I calculate the original value if I know the percentage and the final value?
A: If the final value is the result of adding a percentage to the original value, use the formula: Original Value = Final Value / (1 + Percentage/100). If the final value is the result of subtracting a percentage from the original value, use the formula: Original Value = Final Value / (1 - Percentage/100).
Conclusion
Understanding the percentage of 0.5, which is 50%, is more than just a mathematical exercise; it's a gateway to grasping the broader applications of percentages in everyday life. From calculating discounts and understanding financial data to interpreting statistics and making informed decisions, percentages are an indispensable tool. By mastering the basics of percentage conversion and understanding their practical applications, you can enhance your analytical skills and make more informed decisions in various aspects of your life.
Now that you have a solid understanding of percentages, why not put your knowledge to the test? Try calculating discounts on your next shopping trip, analyze your personal budget using percentages, or explore more advanced statistical concepts. Share your experiences and insights in the comments below, and let's continue to deepen our understanding of this essential mathematical concept together.
Latest Posts
Latest Posts
-
What Are The Factors Of 120
Nov 28, 2025
-
How To Find Median With Even Numbers
Nov 28, 2025
-
What Is The Basic Unit Of Life
Nov 28, 2025
-
What Is The Percentage Of 0 5
Nov 28, 2025
-
Is Length And Height The Same
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.