What Is The Lowest Common Multiple Of 9 And 15
catanddoghelp
Nov 28, 2025 · 10 min read
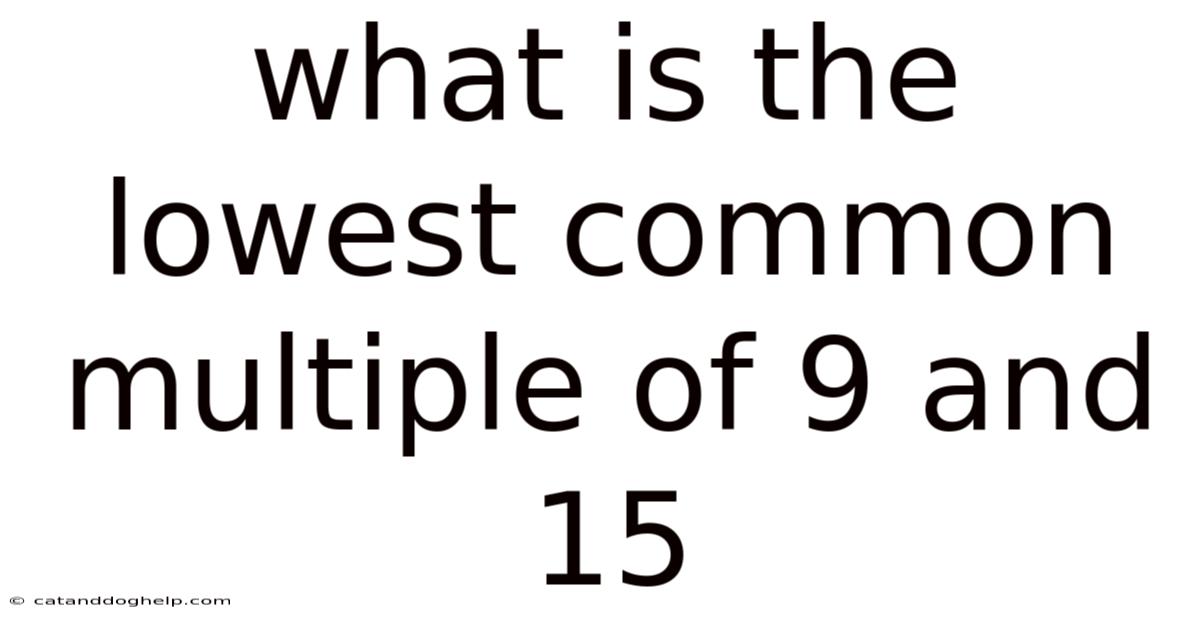
Table of Contents
Imagine you're planning a party and want to serve both hot dogs and hamburgers. Hot dogs come in packs of 9, while hamburger patties come in packs of 15. To avoid having leftovers and ensure everyone gets either a hot dog or a hamburger, you need to figure out the smallest number of each item to buy so that you have the same total number. This is where the concept of the lowest common multiple comes into play.
Calculating the lowest common multiple (LCM) is a fundamental skill in mathematics, with applications extending far beyond party planning. Whether you're simplifying fractions, scheduling events, or solving algebraic equations, understanding how to find the LCM is crucial. In this article, we will explore the process of determining the LCM of 9 and 15, and we'll also provide a detailed explanation of what the LCM is, different methods to calculate it, real-world applications, current trends, and expert advice to help you master this essential mathematical concept.
Main Subheading
Before diving into the specifics of finding the LCM of 9 and 15, let's establish a solid understanding of the concept itself. The lowest common multiple, also known as the least common multiple, is the smallest positive integer that is perfectly divisible by two or more numbers. In simpler terms, it's the smallest number that all given numbers can divide into without leaving a remainder. Understanding this concept involves delving into the realms of multiples, common multiples, and ultimately, the lowest among those common multiples.
The LCM is a foundational concept in number theory and arithmetic, playing a crucial role in various mathematical operations. It provides a basis for simplifying fractions, solving algebraic equations, and understanding number relationships. The LCM also has practical applications in real-world scenarios, such as scheduling events, synchronizing processes, and even in musical theory. Its utility stems from its ability to find the smallest quantity that satisfies a divisibility condition across multiple numbers, making it an indispensable tool in quantitative problem-solving.
Comprehensive Overview
The definition of the lowest common multiple involves a few key concepts, each building upon the last. Let's break these down to get a clearer understanding:
-
Multiples: A multiple of a number is the result of multiplying that number by an integer. For example, multiples of 9 are 9, 18, 27, 36, and so on. Similarly, multiples of 15 are 15, 30, 45, 60, and so on.
-
Common Multiples: A common multiple of two or more numbers is a number that is a multiple of each of those numbers. In other words, it’s a number that each of the given numbers can divide into evenly. For example, common multiples of 9 and 15 include 45, 90, 135, and so on.
-
Lowest Common Multiple: Among all the common multiples of a set of numbers, the lowest common multiple is the smallest one. For 9 and 15, while 45, 90, and 135 are all common multiples, 45 is the smallest, making it the LCM.
The concept of the LCM dates back to ancient mathematical studies. Early mathematicians recognized the importance of finding common units or quantities, which led to the development of methods for finding the LCM. While the exact origins are difficult to pinpoint, the concept has been refined and formalized over centuries, becoming a staple in mathematical curricula worldwide. The ancient Babylonians, Egyptians, and Greeks all had methods for dealing with multiples and divisors, which laid the groundwork for understanding the LCM.
There are several methods to calculate the LCM, each with its own advantages and suitability for different situations:
-
Listing Multiples: This method involves listing the multiples of each number until a common multiple is found. It is straightforward and easy to understand, making it suitable for smaller numbers. For example, listing multiples of 9 (9, 18, 27, 36, 45, ...) and 15 (15, 30, 45, ...) shows that 45 is the first common multiple.
-
Prime Factorization: This method involves breaking down each number into its prime factors and then constructing the LCM by taking the highest power of each prime factor that appears in any of the numbers. For example, 9 = 3^2 and 15 = 3 x 5. The LCM is then 3^2 x 5 = 45.
-
Using the Greatest Common Divisor (GCD): The LCM can also be found using the relationship LCM(a, b) = |a x b| / GCD(a, b), where GCD is the greatest common divisor. First, find the GCD of the two numbers, and then use this formula to calculate the LCM. The GCD of 9 and 15 is 3, so the LCM is (9 x 15) / 3 = 135 / 3 = 45.
-
Division Method: This method involves dividing the numbers by their common prime factors until all the quotients are 1. The LCM is the product of all the divisors used. For 9 and 15, you would first divide both by 3, resulting in 3 and 5. Since 3 and 5 have no common factors, the LCM is 3 x 3 x 5 = 45.
Understanding these different methods allows for flexibility in calculating the LCM based on the numbers involved and personal preference. The prime factorization method is particularly useful for larger numbers, while listing multiples works well for smaller sets.
Trends and Latest Developments
The fundamental concept of the lowest common multiple remains unchanged, but its application and the tools used to calculate it have evolved with technological advancements. Today, numerous online calculators and software tools can quickly compute the LCM of any set of numbers, making it easier than ever to perform complex calculations.
One notable trend is the integration of LCM calculations into educational software and apps. These tools often provide step-by-step solutions, helping students understand the underlying principles while ensuring accuracy. This approach aligns with modern educational strategies that emphasize both conceptual understanding and practical application.
In computer science, the LCM is used in various algorithms related to scheduling, data synchronization, and resource allocation. For instance, in distributed systems, the LCM can help determine the optimal timing for synchronizing tasks across multiple nodes. The increased complexity of modern computing systems has amplified the importance of efficient LCM calculations.
There's also growing interest in exploring the connections between the LCM and other mathematical concepts, such as modular arithmetic and cryptography. These connections offer new avenues for research and potential applications in areas like data security and algorithm optimization.
Professional insights reveal that while calculators and software can expedite the process, a solid understanding of the LCM's theoretical foundations remains crucial. Professionals in fields like engineering, finance, and computer science often encounter situations where they need to apply the LCM in complex problem-solving scenarios. Relying solely on automated tools without understanding the underlying principles can lead to errors or inefficient solutions.
Therefore, current trends emphasize a balanced approach: leveraging technology for quick calculations while maintaining a strong grasp of the mathematical concepts.
Tips and Expert Advice
Calculating the lowest common multiple can be simplified with some practical tips and expert advice. Here are several guidelines to help you master this skill:
-
Master Prime Factorization: A thorough understanding of prime factorization is crucial for efficiently finding the LCM, especially for larger numbers. Practice breaking down numbers into their prime factors until it becomes second nature. Remember that every number can be expressed as a unique product of prime numbers, which simplifies the process of finding common multiples. Regularly practice with different sets of numbers to improve your proficiency.
-
Use the GCD Method Wisely: The relationship between the LCM and the greatest common divisor (GCD) can be a powerful tool. If you already know how to calculate the GCD, using the formula LCM(a, b) = |a x b| / GCD(a, b) can be more efficient than other methods. Familiarize yourself with different techniques for finding the GCD, such as the Euclidean algorithm. This method is particularly useful when dealing with very large numbers.
-
Look for Obvious Multiples: Before diving into complex calculations, quickly scan the numbers for obvious multiples. For example, if one number is a multiple of the other, the larger number is the LCM. Recognizing these relationships can save you time and effort. For instance, if you're finding the LCM of 6 and 12, you can immediately identify 12 as the LCM since it's a multiple of 6.
-
Estimate and Check: After calculating the LCM, take a moment to estimate and check your answer. Ensure that the LCM you found is indeed divisible by all the original numbers. If it's not, recheck your calculations for errors. This simple step can prevent mistakes and reinforce your understanding. For example, if you find the LCM of 9 and 15 to be 30, you'll quickly realize that 30 is not divisible by 9, indicating an error in your calculation.
-
Apply LCM to Real-World Problems: The best way to solidify your understanding of the LCM is to apply it to real-world scenarios. Look for opportunities to use the LCM in everyday situations, such as scheduling tasks, planning events, or even cooking. For instance, if you're trying to coordinate two different tasks that need to be done every 3 days and every 5 days, finding the LCM (which is 15) will tell you when both tasks will coincide next.
-
Use Online Tools Wisely: Online LCM calculators can be helpful for quick calculations, but don't rely on them exclusively. Use them to check your work or to explore more complex problems, but always make sure you understand the underlying principles. Over-reliance on calculators can hinder your ability to solve problems manually and understand the mathematical concepts involved.
By following these tips and continuously practicing, you'll become proficient in finding the lowest common multiple and applying it effectively in various contexts.
FAQ
Q: What is the difference between LCM and GCD?
A: The LCM (lowest common multiple) is the smallest number that is a multiple of two or more numbers. The GCD (greatest common divisor) is the largest number that divides two or more numbers without leaving a remainder. They are related by the formula LCM(a, b) = |a x b| / GCD(a, b).
Q: Can the LCM of two numbers be smaller than both numbers?
A: No, the LCM of two numbers cannot be smaller than either of the numbers. It must be equal to or greater than the largest of the two numbers because it has to be a multiple of both.
Q: What happens if two numbers have no common factors?
A: If two numbers have no common factors other than 1, they are said to be relatively prime. In this case, the LCM is simply the product of the two numbers.
Q: Is there an LCM for more than two numbers?
A: Yes, the LCM can be found for any set of two or more numbers. The process involves finding the smallest number that is a multiple of all the given numbers.
Q: How is LCM used in real life?
A: The LCM is used in various real-life scenarios, such as scheduling events, synchronizing processes, simplifying fractions, and solving problems in engineering, finance, and computer science.
Conclusion
In summary, the lowest common multiple is the smallest positive integer that is divisible by two or more numbers. It is a fundamental concept in mathematics with widespread applications in various fields. We explored the definition of the LCM, different methods to calculate it (listing multiples, prime factorization, using the GCD, and division method), and practical tips to master its computation. Understanding the LCM not only enhances your mathematical skills but also equips you with a valuable tool for solving real-world problems.
Now that you have a comprehensive understanding of the LCM, put your knowledge into practice! Try calculating the LCM of different sets of numbers, explore real-world applications, and share your findings with others. Engage in discussions, solve problems, and continue to deepen your understanding of this essential mathematical concept. Your journey to mastering the LCM has just begun—embrace the challenge and enjoy the process of discovery.
Latest Posts
Latest Posts
-
What Is The Difference Between Electron Geometry And Molecular Geometry
Nov 28, 2025
-
What Is The Multiple Of 7
Nov 28, 2025
-
What Is The Lowest Common Multiple Of 9 And 15
Nov 28, 2025
-
Is Oxygen A Cation Or Anion
Nov 28, 2025
-
Five Letter Word Beginning With E
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.