What Is 1 8 As A Percentage
catanddoghelp
Nov 28, 2025 · 10 min read
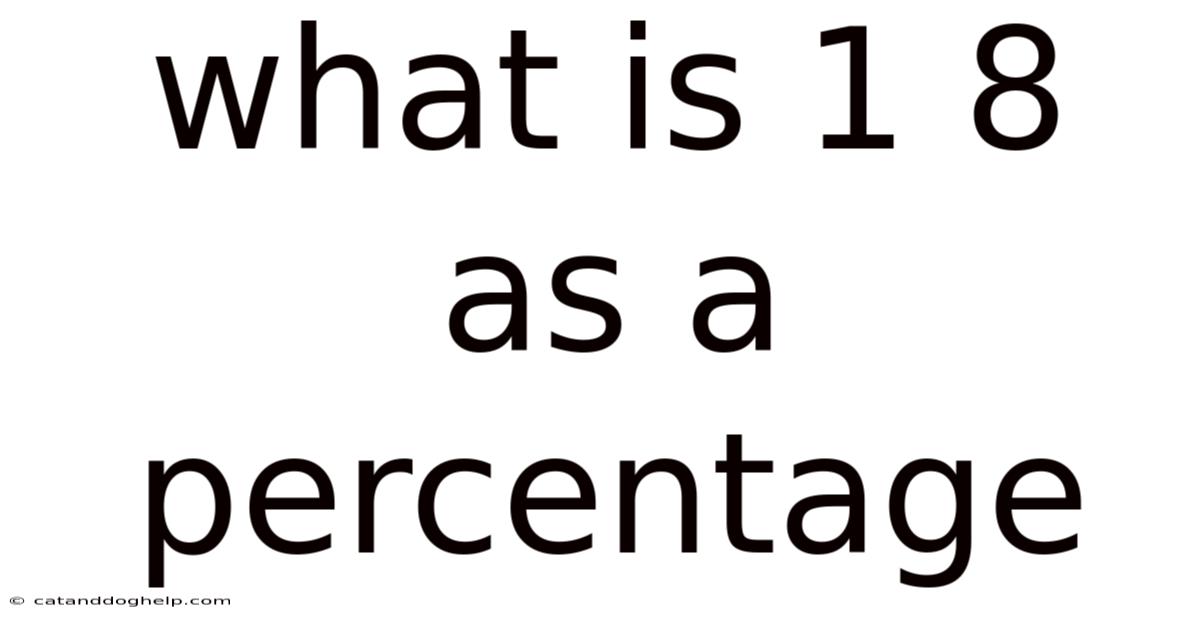
Table of Contents
Imagine you're baking a cake and the recipe calls for a fraction of an ingredient. You might think, "Okay, but how much of the whole thing is that, really?" Understanding how to convert fractions to percentages helps us in everyday situations, from cooking to calculating discounts. It's a practical skill that makes numbers more relatable.
Have you ever wondered how your test scores translate into a percentage? Or perhaps you're curious about the percentage of a pizza you devoured last night? Converting fractions to percentages is a fundamental mathematical skill that bridges the gap between simple fractions and easily understandable proportions. It’s a small conversion, but a powerful tool in understanding proportions and making informed decisions. So, let's dive into understanding what 1/8 is as a percentage, and explore the broader world of fraction-to-percentage conversions.
Understanding Fractions, Decimals, and Percentages
To truly grasp what 1/8 means as a percentage, it's essential to understand the relationship between fractions, decimals, and percentages. These three concepts are different ways of representing the same thing: a part of a whole. Understanding this connection will make converting between them much easier.
A fraction represents a part of a whole, written as one number over another, separated by a line. The number above the line is the numerator, indicating how many parts we have. The number below the line is the denominator, representing the total number of equal parts the whole is divided into. In the fraction 1/8, 1 is the numerator, and 8 is the denominator.
A decimal is another way of representing a part of a whole, using a base-10 system. Decimals use a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half, and 0.25 represents one-quarter. Decimals are particularly useful for precise measurements and calculations.
A percentage is a way of expressing a number as a fraction of 100. The word "percent" means "per hundred," so a percentage tells you how many parts out of 100 you have. For example, 50% means 50 out of 100, or half of the total. Percentages are widely used in everyday life to describe discounts, interest rates, and proportions.
The relationship between these three is that they are interchangeable. A fraction can be converted into a decimal, and a decimal can be converted into a percentage, and vice versa. Knowing how to convert between these forms allows for better understanding and application of numerical data in various contexts. The ability to seamlessly move between fractions, decimals, and percentages enhances mathematical fluency and problem-solving skills.
The Foundation of Fraction-to-Percentage Conversion
The fundamental principle behind converting a fraction to a percentage involves expressing the fraction as an equivalent fraction with a denominator of 100. Since a percentage is essentially a fraction out of 100, finding this equivalent fraction directly gives us the percentage value.
Here’s the basic formula:
Percentage = (Fraction) × 100
This formula works because multiplying a fraction by 100 effectively scales the fraction to a proportion out of 100, which is precisely what a percentage represents. The process involves simple multiplication and can be applied to any fraction to find its percentage equivalent.
Let’s break this down further with an example. Suppose you want to convert the fraction 1/4 to a percentage. Using the formula:
Percentage = (1/4) × 100 = 25%
This means that 1/4 is equivalent to 25 out of 100, or 25%. This method is straightforward and can be used for any fraction, making it a versatile tool for understanding proportions.
Calculating 1/8 as a Percentage
Now that we understand the basics, let's calculate what 1/8 is as a percentage. We'll use the formula:
Percentage = (Fraction) × 100
In this case, our fraction is 1/8, so the calculation is:
Percentage = (1/8) × 100
To solve this, divide 100 by 8:
100 ÷ 8 = 12.5
Therefore, 1/8 as a percentage is 12.5%. This means that 1/8 of something is equal to 12.5 out of 100 parts.
Alternative Method: Converting to Decimal First
Another way to find the percentage is to convert the fraction to a decimal first and then convert the decimal to a percentage. This method can be particularly useful when the fraction doesn't easily convert to a fraction with a denominator of 100.
Step 1: Convert the Fraction to a Decimal
To convert 1/8 to a decimal, divide the numerator (1) by the denominator (8):
1 ÷ 8 = 0.125
So, the decimal equivalent of 1/8 is 0.125.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100:
- 125 × 100 = 12.5%
As you can see, both methods yield the same result: 1/8 is equal to 12.5%.
Real-World Examples of Using Percentages
Percentages are everywhere, and understanding how to work with them is incredibly useful. Here are a few real-world examples to illustrate their importance:
Discounts: When you see a sign that says "20% off," you're dealing with percentages. If an item costs $50 and there's a 20% discount, you calculate the discount amount by finding 20% of $50. This is done by multiplying $50 by 0.20 (the decimal equivalent of 20%), which gives you $10. So, you save $10 on the item.
Test Scores: Test scores are often expressed as percentages. If you get 80 out of 100 questions correct on a test, your score is 80%. This makes it easy to understand your performance relative to the total possible score.
Statistics: In statistics, percentages are used to describe proportions and rates. For example, if a survey finds that 60% of people prefer a certain brand of coffee, it means that out of every 100 people surveyed, 60 prefer that brand.
Financial Investments: Interest rates on savings accounts and loans are expressed as percentages. If a savings account has an annual interest rate of 2%, it means that for every $100 you deposit, you'll earn $2 in interest over the course of a year.
Trends and Latest Developments
In today's data-driven world, the ability to work with percentages is more important than ever. Recent trends show an increasing emphasis on data literacy, which includes understanding and interpreting percentages in various contexts.
Data Visualization: Visualizing data using charts and graphs often involves percentages to represent proportions and trends. For example, pie charts use percentages to show how different categories contribute to a whole.
E-commerce: Online retailers use percentages extensively to display discounts, promotions, and sales tax. Understanding these percentages helps consumers make informed purchasing decisions.
Financial Literacy: There's a growing movement to improve financial literacy, which includes teaching people how to calculate interest rates, understand investment returns, and manage budgets using percentages.
Scientific Research: In scientific studies, percentages are used to report findings, such as the effectiveness of a new drug or the prevalence of a certain condition in a population.
These trends highlight the ongoing importance of understanding percentages and their applications in various fields. Staying up-to-date with these trends can help you make better decisions and understand the world around you more effectively.
Tips and Expert Advice
Converting fractions to percentages can become second nature with practice. Here are some tips and expert advice to help you master this skill:
Memorize Common Fractions: Knowing the percentage equivalents of common fractions like 1/2 (50%), 1/4 (25%), 1/3 (33.33%), and 1/5 (20%) can save you time and effort. These fractions appear frequently, so having their percentage equivalents memorized can speed up your calculations.
Use Mental Math: With practice, you can perform many fraction-to-percentage conversions mentally. For example, to find 25% of a number, you can simply divide the number by 4, since 25% is equivalent to 1/4. Similarly, to find 10% of a number, divide it by 10.
Simplify Fractions: Before converting a fraction to a percentage, simplify it if possible. Simplifying a fraction makes it easier to work with and can reduce the complexity of the calculation. For example, if you need to convert 2/4 to a percentage, simplify it to 1/2 first, which you know is 50%.
Use Online Calculators: When dealing with more complex fractions or when you need to convert a large number of fractions quickly, online calculators can be a valuable tool. Many websites offer free fraction-to-percentage calculators that can provide accurate results in seconds.
Practice Regularly: Like any skill, mastering fraction-to-percentage conversions requires practice. Incorporate these conversions into your daily life by calculating discounts, figuring out tips, and estimating proportions. The more you practice, the more confident you'll become.
Understand the Context: Always consider the context in which you're using percentages. Percentages can be misleading if not interpreted correctly. For example, a large percentage increase on a small base number may not be as significant as it seems.
Frequently Asked Questions (FAQ)
Q: How do I convert a mixed number to a percentage?
A: First, convert the mixed number to an improper fraction. Then, follow the same steps as converting a regular fraction to a percentage: multiply by 100. For example, to convert 2 1/2 to a percentage, first convert it to 5/2. Then, (5/2) × 100 = 250%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This happens when the part is larger than the whole. For example, if a company's sales increase by 150%, it means the sales have more than doubled.
Q: How do I calculate the percentage increase or decrease between two numbers?
A: To calculate the percentage increase or decrease, use the formula: ((New Value - Old Value) / Old Value) × 100. If the result is positive, it's a percentage increase. If it's negative, it's a percentage decrease.
Q: What's the difference between percentage and percentage points?
A: Percentage is a proportion out of 100, while percentage points refer to the difference between two percentages. For example, if an interest rate increases from 5% to 7%, it has increased by 2 percentage points.
Q: How accurate are percentage calculations?
A: The accuracy of percentage calculations depends on the accuracy of the original numbers. In general, it's a good idea to round percentages to a reasonable number of decimal places, depending on the context.
Conclusion
Understanding what 1/8 is as a percentage (12.5%) is more than just a mathematical exercise; it's a practical skill that empowers you to make sense of the world around you. From calculating discounts to interpreting statistics, percentages are an integral part of daily life. By mastering the art of converting fractions to percentages, you gain a valuable tool for understanding proportions and making informed decisions.
Now that you've learned how to convert 1/8 to a percentage and explored the broader applications of percentages, take the next step and apply this knowledge in your everyday life. Try calculating the percentage of a discount on your next purchase, or figure out the percentage of your monthly budget you're allocating to different expenses. The more you practice, the more confident and proficient you'll become. Share this article with friends and family who might benefit from understanding percentages better, and let's empower each other to become more numerate and informed individuals.
Latest Posts
Latest Posts
-
Difference Between Dna Replication And Transcription
Nov 28, 2025
-
33 Cm Is How Many Inches
Nov 28, 2025
-
Least Common Denominator Of 12 And 16
Nov 28, 2025
-
How Many Km In A M
Nov 28, 2025
-
What Is 1 8 As A Percentage
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.