Smallest Common Multiple Of 3 And 4
catanddoghelp
Nov 20, 2025 · 14 min read
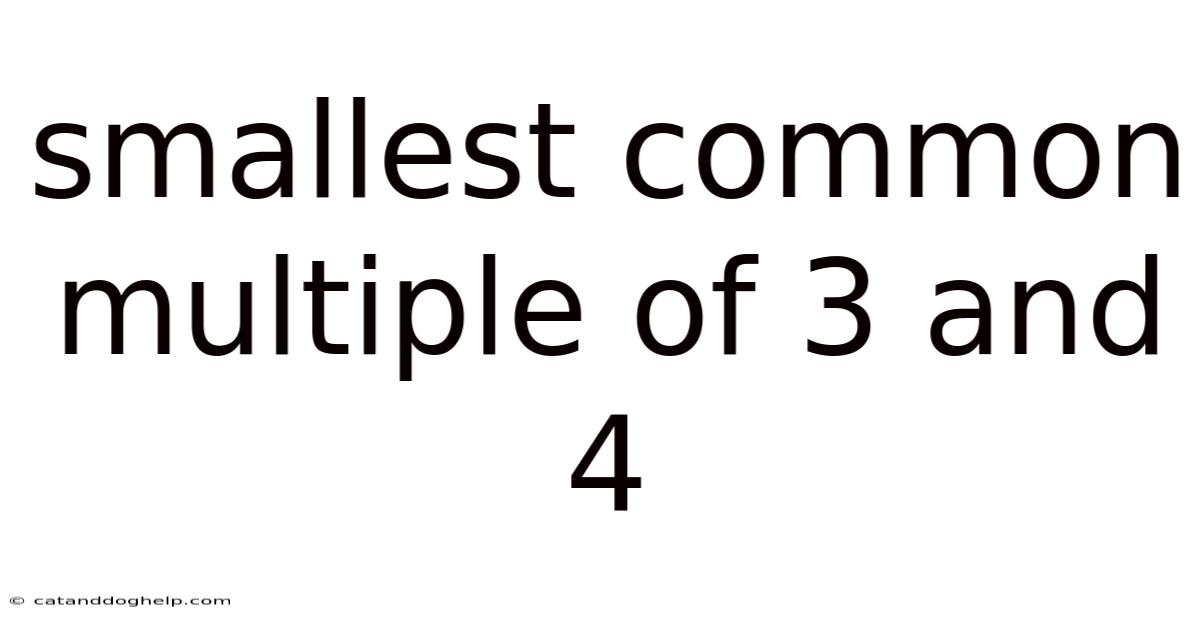
Table of Contents
Have you ever wondered how often you and your friend, who both love running, end up at the park at the same time? You go every three days and your friend goes every four. Finding that overlap isn't just about chance; it’s math in action! This simple scenario introduces a concept that’s incredibly useful in everyday life: the smallest common multiple.
Imagine you're planning a small event and need to buy plates and napkins. Plates come in packs of three, and napkins in packs of four. To avoid waste and ensure you have an equal number of each, you need to figure out the smallest amount you can buy of both. The answer lies in understanding the smallest common multiple of 3 and 4. This mathematical tool isn't just for solving puzzles in textbooks; it simplifies planning, scheduling, and resource management in countless ways.
Main Subheading
The smallest common multiple (SCM), often referred to as the least common multiple (LCM), is a foundational concept in number theory. It appears in various contexts, from basic arithmetic to advanced mathematical problem-solving. At its core, the SCM of two or more numbers is the smallest positive integer that is divisible by each of those numbers without leaving a remainder. For example, when we consider the numbers 3 and 4, their smallest common multiple is 12. This is because 12 is the smallest number that both 3 and 4 divide into evenly.
Understanding the SCM is crucial because it simplifies many mathematical operations, especially those involving fractions and ratios. When adding or subtracting fractions with different denominators, finding the SCM of those denominators allows us to express the fractions with a common denominator, making the operation straightforward. Moreover, the SCM helps in solving real-world problems such as scheduling events, distributing resources, and understanding cyclical phenomena. Its applications extend beyond elementary mathematics, playing a significant role in fields like computer science, engineering, and cryptography, where efficient computation and resource management are paramount.
Comprehensive Overview
To fully grasp the concept of the smallest common multiple, it is essential to delve into its definitions, scientific foundations, historical context, and essential concepts.
Definition of Smallest Common Multiple
The smallest common multiple (SCM) of two or more integers is the smallest positive integer that is a multiple of each of the given integers. In simpler terms, it is the smallest number that all the given numbers divide into evenly. For any two integers a and b, their SCM is denoted as SCM(a, b). If we consider the numbers 3 and 4, the multiples of 3 are 3, 6, 9, 12, 15, 18, and so on, while the multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. The smallest number that appears in both lists is 12, making it the SCM of 3 and 4.
Scientific Foundation
The concept of the SCM is deeply rooted in number theory, a branch of mathematics that deals with the properties and relationships of numbers, particularly integers. Number theory provides the theoretical framework for understanding divisibility, prime numbers, and factorization—all of which are crucial for determining the SCM. The fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely expressed as a product of prime numbers, is particularly important. This theorem allows us to break down numbers into their prime factors, making it easier to find their SCM.
Historical Context
The study of multiples and divisors dates back to ancient civilizations. Early mathematicians in Greece, such as Euclid, explored these concepts extensively. While the term "smallest common multiple" may not have been explicitly used, the underlying ideas were well understood and applied in various mathematical problems. The need to find common measures and proportions in trade, construction, and astronomy drove the development of these concepts. Over time, different cultures and mathematicians refined these ideas, leading to the systematic methods we use today.
Methods to Calculate the Smallest Common Multiple
There are several methods to calculate the SCM of two or more numbers, each with its advantages depending on the specific numbers involved:
-
Listing Multiples: This method involves listing the multiples of each number until a common multiple is found. It is straightforward and easy to understand, making it suitable for small numbers. For example, to find the SCM of 3 and 4, list the multiples of 3 (3, 6, 9, 12, 15, ...) and the multiples of 4 (4, 8, 12, 16, ...). The smallest common multiple is 12.
-
Prime Factorization: This method involves breaking down each number into its prime factors and then combining these factors to find the SCM. First, find the prime factorization of each number. For 3, the prime factorization is simply 3. For 4, the prime factorization is 2 x 2, or 2². Then, take the highest power of each prime factor that appears in any of the factorizations and multiply them together. In this case, we have 2² and 3, so the SCM is 2² x 3 = 4 x 3 = 12.
-
Using the Greatest Common Divisor (GCD): The SCM of two numbers can be calculated using their greatest common divisor (GCD). The formula is:
SCM(a, b) = (|a * b|) / GCD(a, b)
The GCD of 3 and 4 is 1, since 3 and 4 have no common factors other than 1. Therefore, the SCM of 3 and 4 is (|3 * 4|) / 1 = 12.
Essential Concepts Related to SCM
-
Multiple: A multiple of a number is the product of that number and any integer. For example, the multiples of 3 are 3, 6, 9, 12, 15, and so on.
-
Divisor: A divisor of a number is an integer that divides the number evenly, leaving no remainder. For example, the divisors of 12 are 1, 2, 3, 4, 6, and 12.
-
Prime Number: A prime number is an integer greater than 1 that has no positive divisors other than 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on.
-
Prime Factorization: Prime factorization is the process of expressing a number as a product of its prime factors. For example, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3.
-
Greatest Common Divisor (GCD): The greatest common divisor (GCD) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. For example, the GCD of 12 and 18 is 6.
Understanding these definitions, scientific foundations, historical context, and methods for calculation provides a solid basis for appreciating the significance and utility of the smallest common multiple in mathematics and its applications.
Trends and Latest Developments
In recent years, the study and application of the smallest common multiple (SCM) have seen several interesting trends and developments, driven by advancements in technology and the increasing complexity of mathematical problems.
Computational Advancements
With the advent of high-speed computing, algorithms for calculating the SCM have become more efficient and capable of handling very large numbers. Modern computer algebra systems can quickly determine the SCM of multiple large integers, which is particularly useful in fields like cryptography and data compression. These advancements allow for more complex mathematical models and simulations that rely on efficient computation of SCMs.
Educational Approaches
Educators are increasingly focusing on teaching the SCM and related concepts using interactive and visual methods. Online tools, educational software, and gamified learning platforms help students grasp the concept more intuitively. These approaches often involve real-world examples and applications, making the learning process more engaging and relevant.
Interdisciplinary Applications
The SCM is finding new applications in various interdisciplinary fields. In computer science, it is used in scheduling tasks in operating systems and optimizing database queries. In engineering, it helps in synchronizing different components of a system. In music theory, it is used to understand harmonic relationships and rhythmic patterns. The versatility of the SCM ensures its continued relevance in diverse areas of study and practice.
Data Analysis and Optimization
In the realm of data analysis, the SCM is being used to identify patterns and cycles in large datasets. For example, in financial markets, analysts use the SCM to find recurring patterns in stock prices or economic indicators. This can help in making predictions and optimizing investment strategies. Similarly, in logistics and supply chain management, the SCM is used to optimize delivery schedules and inventory management, reducing costs and improving efficiency.
Integration with AI and Machine Learning
As artificial intelligence and machine learning become more prevalent, the SCM is being integrated into algorithms for optimization and pattern recognition. For instance, in scheduling algorithms, AI can use the SCM to find the most efficient way to allocate resources and tasks. In machine learning, the SCM can help in identifying and classifying periodic patterns in data, improving the accuracy of predictive models.
Professional Insights
From a professional standpoint, a deep understanding of the SCM is invaluable in several domains:
- Software Development: Efficient algorithms for calculating the SCM are essential for optimizing code and improving performance. Developers use these algorithms to solve problems related to scheduling, resource allocation, and data synchronization.
- Financial Analysis: Analysts use the SCM to identify patterns and cycles in financial data, helping them make informed investment decisions and manage risk.
- Operations Management: Operations managers use the SCM to optimize supply chain logistics, scheduling, and resource allocation, improving efficiency and reducing costs.
- Education: Educators need a solid understanding of the SCM to effectively teach mathematical concepts and their real-world applications to students.
Staying abreast of these trends and developments ensures that professionals can leverage the power of the SCM in innovative and practical ways, driving efficiency, optimization, and informed decision-making across various fields.
Tips and Expert Advice
Understanding and applying the smallest common multiple (SCM) effectively can greatly simplify various tasks in mathematics and real-world scenarios. Here are some practical tips and expert advice to help you master the concept:
1. Understand the Fundamentals
Before diving into complex problems, ensure you have a solid grasp of the basic definitions and concepts related to the SCM. Know what multiples, divisors, prime numbers, and prime factorization are. This foundational knowledge will make it easier to understand and apply the SCM in different contexts.
- Example: Practice identifying the multiples and divisors of small numbers like 6, 8, and 10. Understand how prime numbers play a crucial role in finding the SCM.
2. Choose the Right Method
There are several methods to calculate the SCM, and the best choice depends on the specific numbers involved. For small numbers, listing multiples might be the simplest approach. For larger numbers, prime factorization or using the GCD is more efficient.
- Example: If you need to find the SCM of 3 and 4, listing multiples (3, 6, 9, 12, ...) and (4, 8, 12, ...) is straightforward. However, for finding the SCM of 24 and 36, prime factorization (24 = 2³ x 3 and 36 = 2² x 3²) is quicker.
3. Practice Prime Factorization
Prime factorization is a powerful tool for finding the SCM, especially for larger numbers. Practice breaking down numbers into their prime factors. This skill is essential for efficiently calculating the SCM and solving related problems.
- Example: Practice finding the prime factorization of numbers like 48, 72, and 100. This will help you become more comfortable with the process and improve your speed.
4. Use the GCD to Simplify Calculations
The relationship between the SCM and the greatest common divisor (GCD) can simplify calculations. Use the formula SCM(a, b) = (|a * b|) / GCD(a, b) to find the SCM when you know the GCD.
- Example: To find the SCM of 16 and 24, first find their GCD, which is 8. Then, use the formula: SCM(16, 24) = (|16 * 24|) / 8 = 384 / 8 = 48.
5. Apply SCM in Real-World Problems
Understanding the SCM is not just about solving mathematical problems; it's also about applying it to real-world scenarios. Look for opportunities to use the SCM in everyday situations, such as scheduling events, managing resources, and optimizing processes.
- Example: Suppose you want to schedule a meeting that occurs every 3 days and another that occurs every 4 days. To find the next day when both meetings will occur, calculate the SCM of 3 and 4, which is 12. This means both meetings will occur together every 12 days.
6. Break Down Complex Problems
When faced with complex problems involving the SCM, break them down into smaller, more manageable parts. Identify the key numbers and relationships, and then apply the appropriate methods to find the SCM.
- Example: If you need to find the SCM of three numbers, such as 6, 8, and 10, first find the SCM of two of them (e.g., SCM of 6 and 8 is 24), and then find the SCM of the result and the remaining number (SCM of 24 and 10 is 120).
7. Utilize Online Tools and Resources
Take advantage of online tools and resources to check your work and explore different approaches to solving SCM problems. Many websites and apps offer calculators and tutorials that can help you improve your understanding and skills.
- Example: Use online SCM calculators to verify your answers and explore different problem-solving techniques. Look for educational videos and tutorials that explain the concept in a visual and engaging way.
8. Practice Regularly
Like any mathematical skill, mastering the SCM requires regular practice. Set aside time to work through various problems and examples. The more you practice, the more comfortable and confident you will become.
- Example: Dedicate 15-20 minutes each day to solving SCM problems. Start with simple examples and gradually work your way up to more complex ones.
9. Seek Help When Needed
Don't hesitate to ask for help from teachers, tutors, or classmates if you are struggling with the SCM. Explaining your difficulties and discussing the concept with others can help you gain a better understanding.
- Example: Join a study group or online forum where you can ask questions and share your experiences with others. Learning from others can provide valuable insights and perspectives.
By following these tips and expert advice, you can develop a strong understanding of the smallest common multiple and its applications. Practice regularly, apply the concept in real-world scenarios, and don't be afraid to seek help when needed.
FAQ
Q: What is the difference between SCM and GCD?
A: The smallest common multiple (SCM) is the smallest positive integer that is a multiple of two or more numbers. The greatest common divisor (GCD) is the largest positive integer that divides two or more numbers without leaving a remainder. SCM looks for a common multiple, while GCD looks for a common divisor.
Q: How do I find the SCM of more than two numbers?
A: To find the SCM of more than two numbers, you can first find the SCM of two of the numbers, and then find the SCM of the result and the remaining number. Repeat this process until you have found the SCM of all the numbers.
Q: Can the SCM of two numbers be smaller than the numbers themselves?
A: No, the SCM of two numbers cannot be smaller than either of the numbers themselves. It must be at least as large as the largest of the numbers.
Q: Is there a formula for finding the SCM?
A: Yes, the formula for finding the SCM of two numbers a and b using their greatest common divisor (GCD) is: SCM(a, b) = (|a * b|) / GCD(a, b).
Q: Why is the SCM important?
A: The SCM is important because it simplifies many mathematical operations, especially those involving fractions and ratios. It also has practical applications in scheduling, resource management, and various other fields.
Conclusion
The smallest common multiple is a fundamental concept in mathematics with widespread applications. Whether you're synchronizing schedules, optimizing resource allocation, or simply trying to understand numerical relationships, the SCM provides a powerful tool for problem-solving. By understanding its definition, methods of calculation, and real-world applications, you can enhance your mathematical toolkit and tackle complex problems with confidence.
Ready to put your knowledge into practice? Try solving SCM problems in your daily life. Can you figure out when your weekly tasks will align perfectly? Share your experiences and challenge others in the comments below. Let's explore the endless possibilities of the smallest common multiple together!
Latest Posts
Latest Posts
-
What Are All The Factors Of 28
Nov 20, 2025
-
What Are The Factors For 72
Nov 20, 2025
-
What Is All The Factors Of 54
Nov 20, 2025
-
Five Letter Word That Ends With T
Nov 20, 2025
-
What Are All The Factors Of 30
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about Smallest Common Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.