What Is The Least Common Multiple Of 6 And 10
catanddoghelp
Nov 20, 2025 · 12 min read
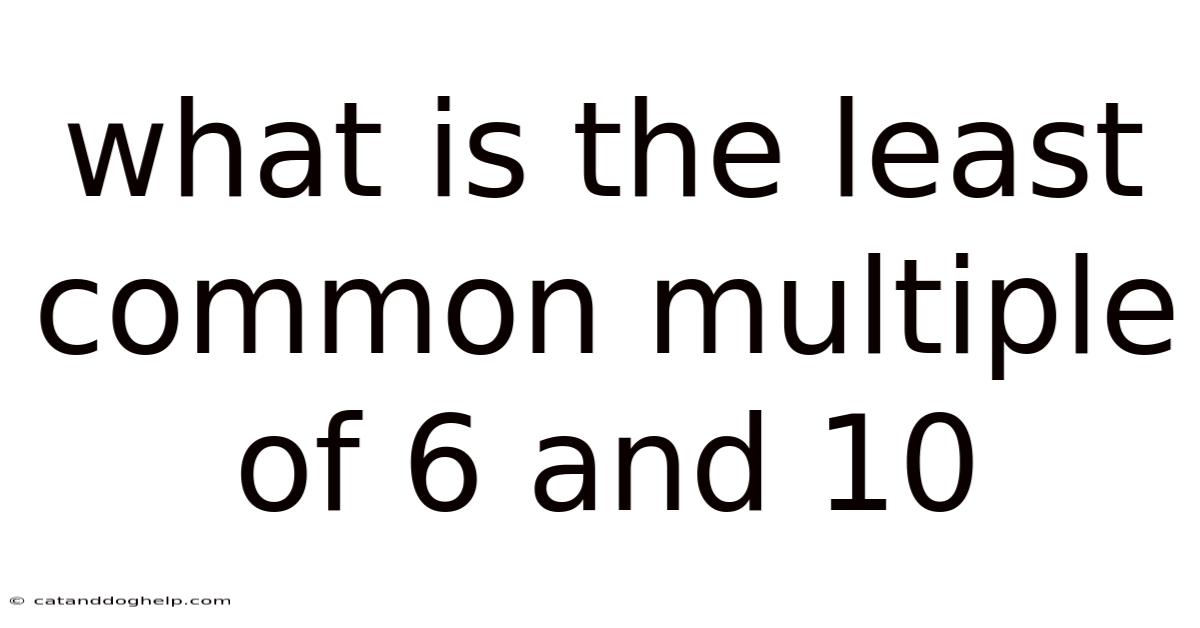
Table of Contents
Imagine you're a baker, and you need to buy cupcake liners and decorative sprinkles. The liners come in packs of 6, and the sprinkles come in packs of 10. You want to buy the smallest number of each so that you have exactly the same amount of liners and sprinkles, with none left over. How many packs of each do you need? This is where the concept of the least common multiple, or LCM, comes into play.
In mathematics, the least common multiple of two or more numbers is the smallest positive integer that is perfectly divisible by each of those numbers. It's a fundamental concept with applications that extend far beyond baking, influencing areas like scheduling, engineering, and even music. Let's explore the concept of the least common multiple of 6 and 10 and its real-world applications.
Understanding the Least Common Multiple
The least common multiple (LCM) is the smallest positive integer that is divisible by two or more integers without any remainder. It is a fundamental concept in number theory and is used extensively in various mathematical and real-world applications. Understanding the LCM is essential for solving problems related to fractions, ratios, and divisibility.
Definition and Basic Concepts
The LCM of two or more numbers is the smallest number that each of the given numbers can divide into evenly. In other words, it's the smallest number that is a multiple of each of the numbers you started with.
For example, consider the numbers 6 and 10. Multiples of 6 are 6, 12, 18, 24, 30, 36, and so on. Multiples of 10 are 10, 20, 30, 40, 50, and so on. The smallest number that appears in both lists is 30. Therefore, the LCM of 6 and 10 is 30.
Importance in Mathematics
The LCM is not just a theoretical concept; it has significant practical applications. Here are a few reasons why understanding the LCM is important:
- Simplifying Fractions: The LCM is crucial when adding or subtracting fractions with different denominators. By finding the LCM of the denominators, you can rewrite the fractions with a common denominator, making the addition or subtraction straightforward.
- Solving Equations: The LCM can be used to clear fractions from equations, making them easier to solve.
- Divisibility Problems: Understanding the LCM helps in solving problems related to divisibility, such as finding the smallest number that satisfies certain divisibility conditions.
- Real-World Applications: As we'll see, the LCM is used in various real-world scenarios, from scheduling to engineering.
Methods for Finding the LCM
There are several methods for finding the LCM of two or more numbers, including:
- Listing Multiples: This involves listing the multiples of each number until you find a common multiple. While simple, this method can be time-consuming for larger numbers.
- Prime Factorization: This method involves breaking down each number into its prime factors and then using those factors to construct the LCM.
- Division Method: This is a systematic approach that involves dividing the numbers by their common prime factors until all numbers are reduced to 1.
Comprehensive Overview of LCM(6, 10)
To comprehensively understand the LCM of 6 and 10, we delve into its definitions, mathematical foundations, and practical methods to compute it. This exploration not only solidifies the theoretical understanding but also provides a toolkit for tackling various mathematical problems.
Prime Factorization Method
The prime factorization method is a powerful technique for finding the LCM. It involves expressing each number as a product of its prime factors and then combining those factors to find the LCM.
Here’s how to apply this method to find the LCM of 6 and 10:
- Prime Factorization of 6:
- 6 = 2 × 3
- Prime Factorization of 10:
- 10 = 2 × 5
- Constructing the LCM:
To find the LCM, take the highest power of each prime factor that appears in either factorization:
- 2 appears in both factorizations, with a highest power of 2¹ (or simply 2).
- 3 appears in the factorization of 6 with a power of 3¹.
- 5 appears in the factorization of 10 with a power of 5¹. Therefore, the LCM of 6 and 10 is 2 × 3 × 5 = 30.
Listing Multiples Method
The listing multiples method is a straightforward way to find the LCM, especially useful for smaller numbers. It involves listing the multiples of each number until a common multiple is found.
Here’s how to apply this method to find the LCM of 6 and 10:
- List Multiples of 6:
- 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- List Multiples of 10:
- 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
- Identify the Least Common Multiple: By comparing the lists, we find that the smallest number that appears in both lists is 30. Therefore, the LCM of 6 and 10 is 30.
Division Method
The division method is a systematic way to find the LCM by dividing the numbers by their common prime factors until all numbers are reduced to 1.
Here’s how to apply this method to find the LCM of 6 and 10:
- Set up the division:
Write 6 and 10 side by side:
2 | 6 10 | 3 5 - Divide by the smallest prime factor that divides both numbers (if any):
Both 6 and 10 are divisible by 2:
2 | 6 10 | 3 5 - Continue dividing by prime factors:
Since 3 and 5 have no common prime factors, we divide each by its own prime factor:
3 | 3 5 | 1 5 5 | 1 5 | 1 1 - Multiply the divisors: The LCM is the product of the divisors: 2 × 3 × 5 = 30.
Relationship between LCM and Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are related by a simple formula:
LCM(a, b) × GCD(a, b) = |a × b|
Where:
- LCM(a, b) is the least common multiple of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
- |a × b| is the absolute value of the product of a and b.
For 6 and 10:
- GCD(6, 10) = 2
- LCM(6, 10) = (6 × 10) / GCD(6, 10) = 60 / 2 = 30
This relationship provides an alternative way to calculate the LCM if you know the GCD, or vice versa.
Properties of LCM
Understanding the properties of LCM can further enhance its comprehension and application:
- Commutative Property: The order of the numbers does not affect the LCM. LCM(a, b) = LCM(b, a) Example: LCM(6, 10) = LCM(10, 6) = 30
- Associative Property: The LCM of multiple numbers can be found by grouping them. LCM(a, b, c) = LCM(LCM(a, b), c) Example: LCM(6, 10, 15) = LCM(30, 15) = 30
- LCM of a Number with Itself: The LCM of a number with itself is the number itself. LCM(a, a) = a Example: LCM(6, 6) = 6
- LCM of 1 with Any Number: The LCM of 1 with any number is the number itself. LCM(1, a) = a Example: LCM(1, 6) = 6
Trends and Latest Developments
The concept of the least common multiple is timeless and fundamental. However, recent trends focus on optimizing algorithms for computing LCMs of large numbers and exploring their applications in emerging fields.
Algorithmic Optimizations
Traditional methods for finding the LCM, such as listing multiples or using prime factorization, can be inefficient for large numbers. Modern algorithms focus on optimizing the computation of LCM using efficient techniques like the Euclidean algorithm for finding the GCD and then applying the relationship LCM(a, b) = |a × b| / GCD(a, b).
Applications in Cryptography
LCM and GCD play a crucial role in various cryptographic algorithms. For instance, the RSA algorithm relies on the properties of prime numbers and their multiples to ensure secure data transmission. Understanding the LCM helps in analyzing and optimizing these cryptographic systems.
Integration with Computational Tools
With the rise of computational tools like Python, MATLAB, and Mathematica, finding the LCM has become more accessible. These tools provide built-in functions for computing the LCM, making it easier to apply the concept in various projects.
Educational Trends
In mathematics education, there is a growing emphasis on teaching the LCM through real-world applications and interactive tools. This approach helps students grasp the concept more intuitively and appreciate its practical significance.
Tips and Expert Advice
Understanding the least common multiple is more than just memorizing formulas. Here are some practical tips and expert advice to help you master the concept and apply it effectively.
Tip 1: Understand the Underlying Concept
Advice: Don't just memorize the methods for finding the LCM. Focus on understanding what the LCM represents and why it's important.
Explanation: The LCM is the smallest multiple that two or more numbers share. Visualizing this concept can help you solve problems more intuitively. For example, think of the cupcake liner and sprinkles problem: you need to find the smallest quantity of each so you can have equal amounts.
Tip 2: Practice Different Methods
Advice: Familiarize yourself with various methods for finding the LCM, such as prime factorization, listing multiples, and the division method.
Explanation: Each method has its strengths and weaknesses. Prime factorization is efficient for larger numbers, while listing multiples is easier for smaller numbers. The division method provides a systematic approach that works well in many cases. Practice each method to determine which one you prefer and when to use it.
Tip 3: Use Prime Factorization for Large Numbers
Advice: When dealing with larger numbers, prime factorization is generally the most efficient method.
Explanation: Prime factorization breaks down each number into its prime factors, making it easier to identify common multiples. This method avoids the need to list out potentially long sequences of multiples, saving time and reducing the risk of errors.
Tip 4: Relate LCM to Real-World Problems
Advice: Try to relate the concept of the LCM to real-world scenarios.
Explanation: Understanding how the LCM applies to everyday situations can make the concept more relatable and easier to remember. Examples include scheduling events, dividing items into equal groups, and solving problems involving fractions and ratios.
Tip 5: Use Online Calculators to Check Your Work
Advice: Utilize online LCM calculators to verify your answers and identify any mistakes.
Explanation: Online calculators can be a valuable tool for checking your work and reinforcing your understanding of the LCM. They can also help you quickly find the LCM of multiple numbers or very large numbers.
Tip 6: Understand the Relationship Between LCM and GCD
Advice: Recognize the relationship between the LCM and the GCD (Greatest Common Divisor).
Explanation: The formula LCM(a, b) × GCD(a, b) = |a × b| can be a powerful tool for finding the LCM if you know the GCD, or vice versa. Understanding this relationship can provide a shortcut for solving certain problems.
Tip 7: Practice with Different Types of Problems
Advice: Solve a variety of problems involving the LCM to build your skills and confidence.
Explanation: Practice with different types of problems, such as finding the LCM of two numbers, finding the LCM of three or more numbers, and solving word problems that involve the LCM. This will help you develop a deeper understanding of the concept and improve your problem-solving abilities.
Tip 8: Avoid Common Mistakes
Advice: Be aware of common mistakes when finding the LCM and take steps to avoid them.
Explanation: Common mistakes include:
- Forgetting to include all prime factors when using prime factorization.
- Listing only a few multiples and assuming you've found the smallest common multiple.
- Making arithmetic errors when dividing or multiplying.
Double-check your work and use online calculators to verify your answers.
Tip 9: Simplify Fractions Using LCM
Advice: Use the LCM to simplify fractions when adding or subtracting them.
Explanation: When adding or subtracting fractions with different denominators, find the LCM of the denominators to create a common denominator. This makes the addition or subtraction straightforward.
Tip 10: Teach Others
Advice: Try teaching the concept of the LCM to someone else.
Explanation: Teaching is a great way to reinforce your own understanding. Explaining the concept to someone else forces you to think about it in a new way and identify any gaps in your knowledge.
FAQ
Q: What is the least common multiple (LCM)?
A: The least common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by each of those numbers without any remainder.
Q: How do you find the LCM of 6 and 10?
A: You can find the LCM of 6 and 10 using several methods, including:
- Listing multiples: List the multiples of each number until you find a common multiple (30).
- Prime factorization: Find the prime factors of each number (6 = 2 × 3, 10 = 2 × 5) and multiply the highest powers of each prime factor (2 × 3 × 5 = 30).
- Division method: Divide the numbers by their common prime factors until all numbers are reduced to 1, then multiply the divisors.
Q: Why is the LCM important?
A: The LCM is important for simplifying fractions, solving equations, solving divisibility problems, and in various real-world applications such as scheduling and engineering.
Q: Can the LCM be smaller than the numbers you're finding it for?
A: No, the LCM is always greater than or equal to the largest of the numbers you're finding it for.
Q: Is there a relationship between the LCM and the greatest common divisor (GCD)?
A: Yes, the LCM and GCD are related by the formula: LCM(a, b) × GCD(a, b) = |a × b|.
Q: What are some real-world applications of the LCM?
A: Real-world applications of the LCM include scheduling events, dividing items into equal groups, and solving problems involving fractions and ratios.
Conclusion
Understanding the least common multiple is more than just a mathematical exercise; it's a practical skill with applications in various fields. Whether you're a student grappling with fractions or a professional scheduling events, the LCM provides a valuable tool for solving problems efficiently. By mastering the techniques for finding the LCM and understanding its underlying principles, you can enhance your mathematical abilities and tackle real-world challenges with confidence.
Now that you have a solid understanding of the least common multiple of 6 and 10, take the next step! Practice solving LCM problems and explore real-world applications to deepen your knowledge. Share this article with friends or colleagues who might benefit from learning about the LCM, and leave a comment below sharing your experiences or any questions you still have. Let’s continue to explore the fascinating world of mathematics together!
Latest Posts
Latest Posts
-
Which One Of The Following Is A Chemical Change
Nov 20, 2025
-
Greater Than Less Than Sign Calculator
Nov 20, 2025
-
Words That Have Ing At The End
Nov 20, 2025
-
Five Letter Words Starting With K
Nov 20, 2025
-
Rules For Adding And Subtracting Integers
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.