What Is The Least Common Multiple Of 10 And 12
catanddoghelp
Nov 19, 2025 · 11 min read
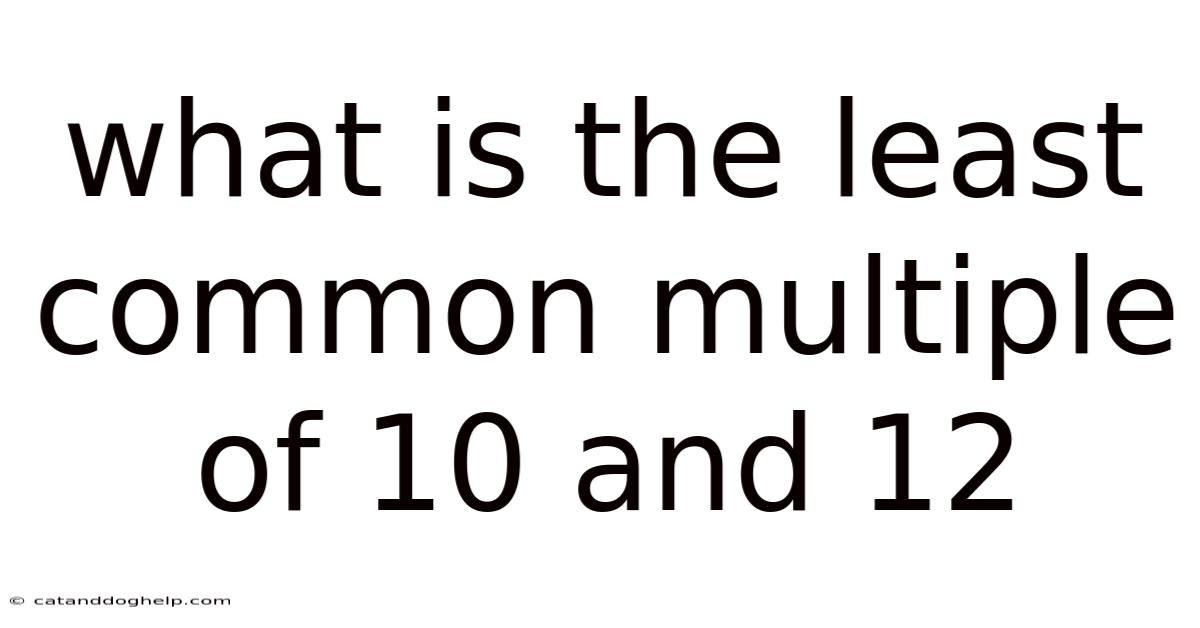
Table of Contents
Have you ever found yourself organizing a party, trying to figure out how many of each item you need so that everything matches up perfectly? Or perhaps you’ve been scheduling events, ensuring that different activities align at specific intervals? These scenarios, seemingly different, share a common mathematical thread: the least common multiple.
Imagine you are setting up a row of holiday lights. One strand blinks every 10 seconds, and another blinks every 12 seconds. You want to know when they will blink together again. This isn't just a matter of curiosity; it's a practical question that highlights the importance of the least common multiple in everyday life. Understanding how to find the least common multiple (LCM) of numbers like 10 and 12 can simplify many real-world problems, from planning events to managing resources. So, let’s dive into the world of LCM and explore how it helps us make sense of patterns and cycles around us.
Main Subheading
The least common multiple (LCM) is a fundamental concept in number theory that helps simplify various mathematical problems. The LCM of two or more numbers is the smallest positive integer that is divisible by each of the numbers. It's a basic idea with wide-ranging uses, from simple arithmetic to complex algebra and real-world applications. Understanding the LCM can significantly improve problem-solving skills and provide insights into numerical relationships.
Finding the LCM is crucial in many mathematical operations, especially when dealing with fractions. When adding or subtracting fractions with different denominators, you need to find a common denominator. The least common denominator (LCD) is simply the LCM of the denominators, making the process of adding or subtracting fractions much easier. It ensures that you are working with the smallest possible numbers, reducing the complexity of the calculations.
Comprehensive Overview
To understand the least common multiple (LCM), let’s first define some key terms and concepts. A multiple of a number is the result of multiplying that number by an integer. For example, the multiples of 10 are 10, 20, 30, 40, and so on. Similarly, the multiples of 12 are 12, 24, 36, 48, and so on. A common multiple of two or more numbers is a number that is a multiple of each of those numbers. For instance, the common multiples of 10 and 12 include 60, 120, 180, and so forth. The least common multiple is the smallest of these common multiples.
The formal definition of the LCM of two integers, a and b, is the smallest positive integer that is divisible by both a and b. Mathematically, it is often denoted as LCM(a, b). The LCM is always a positive integer and is unique for any given set of numbers. The concept extends to more than two numbers as well. For example, the LCM of three numbers a, b, and c is the smallest positive integer divisible by a, b, and c.
The historical roots of the LCM concept can be traced back to ancient mathematics. Early mathematicians recognized the importance of understanding multiples and divisors for solving practical problems related to trade, measurement, and astronomy. While the term "least common multiple" may not have been explicitly used in ancient texts, the underlying idea was present in various forms. For instance, ancient Babylonian and Egyptian mathematicians used concepts related to multiples and divisors in their calculations involving fractions and proportions.
There are several methods to find the LCM of two or more numbers. One common method is listing the multiples of each number until a common multiple is found. For example, to find the LCM of 10 and 12, you could list the multiples of 10 (10, 20, 30, 40, 50, 60, ...) and the multiples of 12 (12, 24, 36, 48, 60, ...). The smallest number that appears in both lists is 60, so LCM(10, 12) = 60.
Another method involves using prime factorization. Prime factorization is the process of breaking down a number into its prime factors. For example, the prime factorization of 10 is 2 × 5, and the prime factorization of 12 is 2 × 2 × 3, or 2² × 3. To find the LCM using prime factorization, you identify the highest power of each prime factor that appears in any of the numbers. In this case, the prime factors are 2, 3, and 5. The highest power of 2 is 2² (from 12), the highest power of 3 is 3¹ (from 12), and the highest power of 5 is 5¹ (from 10). Multiplying these together gives the LCM: 2² × 3 × 5 = 4 × 3 × 5 = 60.
A third method involves using the greatest common divisor (GCD). The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder. The relationship between the LCM and GCD is expressed by the formula: LCM(a, b) = |a × b| / GCD(a, b) To find the LCM of 10 and 12 using this method, you first find the GCD of 10 and 12, which is 2. Then, you multiply 10 and 12 to get 120, and divide by the GCD: 120 / 2 = 60.
Trends and Latest Developments
The concept of the least common multiple (LCM) remains a fundamental part of mathematics education and continues to find relevance in various modern applications. In education, understanding LCM is essential for students as they progress through arithmetic and algebra. It forms a building block for more advanced topics such as number theory and abstract algebra. Educators are continuously looking for innovative ways to teach LCM, incorporating real-world examples and interactive tools to make the concept more engaging and accessible for students.
In recent years, there has been an increasing emphasis on using technology to enhance the learning and application of LCM. Various online tools and software applications are designed to calculate the LCM of numbers quickly and accurately. These tools are particularly useful for students and professionals who need to work with LCM in complex calculations. Additionally, educational platforms often include interactive exercises and simulations that help students visualize and understand the concept of LCM in a more intuitive way.
One notable trend is the use of LCM in computer science and engineering. In areas such as scheduling and synchronization, LCM is used to determine the optimal timing for events or processes. For example, in real-time operating systems, LCM can be used to schedule tasks that need to be executed at regular intervals. By finding the LCM of the intervals, engineers can ensure that tasks are synchronized efficiently and that system resources are utilized effectively.
Another area where LCM is increasingly relevant is in cryptography. While LCM itself may not be directly used in encryption algorithms, the underlying principles of number theory, including LCM and GCD, are crucial for understanding and developing cryptographic systems. Cryptography relies heavily on the properties of prime numbers and their multiples, and a solid understanding of LCM can aid in the analysis and design of cryptographic protocols.
Moreover, LCM finds applications in fields such as music theory and signal processing. In music, LCM can be used to analyze rhythmic patterns and harmonies. For example, when combining different musical phrases with varying lengths, understanding the LCM of their lengths can help create coherent and structured compositions. In signal processing, LCM can be used to analyze periodic signals and identify common frequencies. This is particularly useful in applications such as audio processing and image analysis.
Tips and Expert Advice
Finding the least common multiple (LCM) can be straightforward with the right strategies. Here are some practical tips and expert advice to help you master the concept and apply it effectively in various situations.
Understand the Basics: Before diving into complex calculations, ensure you have a solid grasp of the fundamental concepts. Know the definitions of multiples, common multiples, and the least common multiple. Practice identifying multiples of different numbers and recognizing common multiples. This foundational knowledge will make it easier to understand and apply more advanced techniques for finding the LCM.
Use Prime Factorization: Prime factorization is a powerful method for finding the LCM, especially for larger numbers. Break down each number into its prime factors, and then identify the highest power of each prime factor that appears in any of the numbers. Multiply these highest powers together to find the LCM. This method is systematic and reliable, and it helps avoid errors that can occur when listing multiples manually. For example, to find the LCM of 24 and 36, first find their prime factorizations: 24 = 2³ × 3 36 = 2² × 3² The highest power of 2 is 2³, and the highest power of 3 is 3². Therefore, the LCM(24, 36) = 2³ × 3² = 8 × 9 = 72.
Leverage the GCD Relationship: The relationship between the LCM and the greatest common divisor (GCD) can be a useful shortcut. Remember the formula: LCM(a, b) = |a × b| / GCD(a, b). If you can easily find the GCD of two numbers, you can use this formula to calculate the LCM quickly. This method is particularly helpful when dealing with numbers that have a relatively small GCD. For example, to find the LCM of 15 and 25, first find their GCD, which is 5. Then, multiply 15 and 25 to get 375, and divide by the GCD: 375 / 5 = 75. Therefore, LCM(15, 25) = 75.
List Multiples Strategically: When listing multiples, start with the larger number and check if its multiples are also multiples of the smaller number. This can save time and effort. For example, when finding the LCM of 8 and 12, start by listing the multiples of 12 (12, 24, 36, 48, ...). Check if each multiple is divisible by 8. You'll find that 24 is the first multiple of 12 that is also a multiple of 8, so LCM(8, 12) = 24.
Use Online Calculators: There are many online LCM calculators available that can quickly find the LCM of two or more numbers. These tools are useful for verifying your calculations or for finding the LCM of numbers that are difficult to work with manually. However, it's important to understand the underlying principles and methods for finding the LCM, rather than relying solely on calculators.
Apply LCM in Real-World Problems: Practice applying the concept of LCM in real-world scenarios. This will help you understand its practical significance and improve your problem-solving skills. For example, consider problems involving scheduling, resource allocation, or pattern recognition. By recognizing the role of LCM in these situations, you can develop a deeper appreciation for its usefulness.
Check Your Work: Always double-check your calculations to ensure accuracy. Make sure that the number you have identified as the LCM is indeed a multiple of all the given numbers and that it is the smallest such multiple. This will help you avoid common errors and build confidence in your ability to find the LCM correctly.
FAQ
Q: What is the least common multiple (LCM)? A: The least common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by each of those numbers.
Q: How do I find the LCM of two numbers? A: You can find the LCM by listing multiples, using prime factorization, or using the relationship between LCM and GCD: LCM(a, b) = |a × b| / GCD(a, b).
Q: What is the difference between LCM and GCD? A: The LCM is the smallest multiple that two numbers share, while the GCD is the largest divisor that two numbers share.
Q: Why is the LCM important? A: The LCM is important for simplifying fractions, solving scheduling problems, and understanding patterns in various fields like computer science and music theory.
Q: Can the LCM be larger than the numbers themselves? A: Yes, the LCM is typically larger than the numbers, unless one number is a multiple of the other.
Conclusion
Understanding the least common multiple (LCM) is more than just a mathematical exercise; it's a practical skill that simplifies problem-solving in various real-world scenarios. From scheduling events and synchronizing processes to simplifying fractions and analyzing patterns, the LCM helps us make sense of numerical relationships and optimize our approaches. By mastering the techniques for finding the LCM, such as listing multiples, using prime factorization, and leveraging the GCD relationship, you can enhance your mathematical toolkit and tackle a wide range of challenges with confidence.
Ready to put your knowledge to the test? Try applying the methods discussed in this article to find the LCM of different sets of numbers. Share your findings and any interesting applications you discover in the comments below. Your insights can help others deepen their understanding of the least common multiple and its practical uses. Let's continue exploring the fascinating world of mathematics together!
Latest Posts
Latest Posts
-
Why Is Resource Planning A Complex Process
Nov 19, 2025
-
What Are The Factors Of 40
Nov 19, 2025
-
How Many 1 Gallon In A Liter
Nov 19, 2025
-
Roman Numerals That Multiply To 35
Nov 19, 2025
-
Six Letter Words That Start With S
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 10 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.