Least Common Multiple Of 4 And 6
catanddoghelp
Nov 20, 2025 · 10 min read
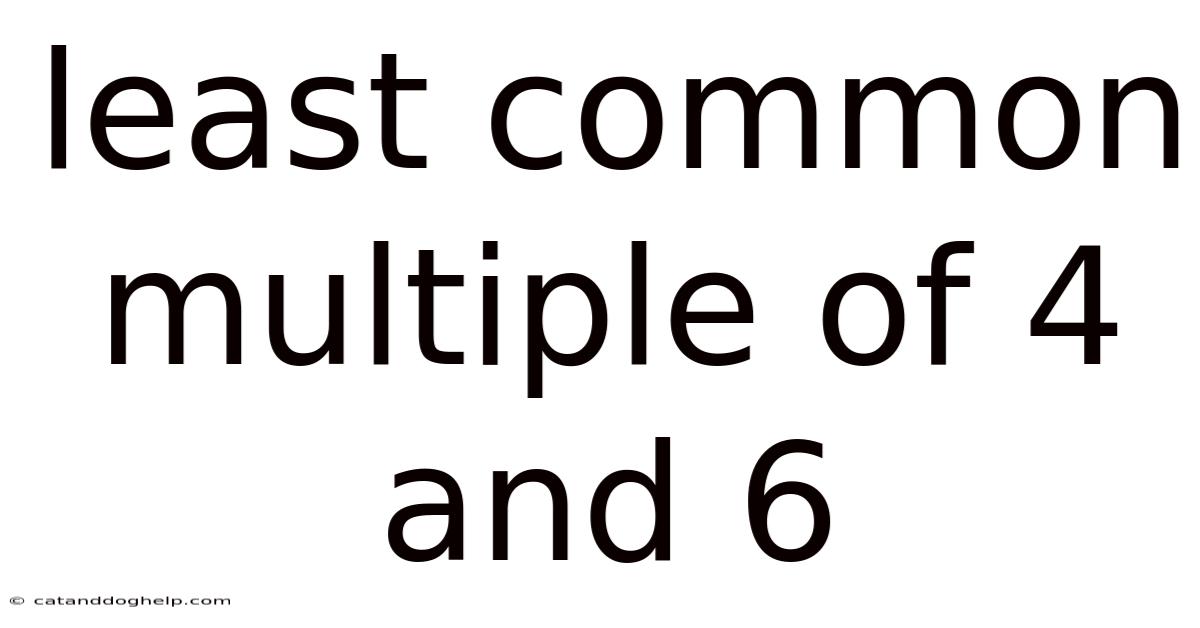
Table of Contents
Have you ever found yourself trying to figure out when two different events will coincide? Perhaps you're coordinating a group project where tasks have varying deadlines, or maybe you're planning a party and need to ensure different deliveries arrive at the same time. This common dilemma often requires finding a common multiple, and that's where the concept of the least common multiple (LCM) comes in handy.
The least common multiple (LCM) is a fundamental concept in mathematics that helps us find the smallest positive integer that is divisible by two or more given numbers. Whether you're a student grappling with number theory or someone looking to simplify everyday calculations, understanding the LCM is invaluable. Let's delve into the world of LCM and explore how to find the LCM of 4 and 6, along with its applications and significance.
Main Subheading: Understanding the Basics of Least Common Multiple (LCM)
The least common multiple (LCM) is defined as the smallest positive integer that is perfectly divisible by each of the given numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. Understanding the LCM is crucial not only for mathematical problem-solving but also for real-world applications that require synchronization or coordination of events with different cycles.
For instance, consider two gears in a machine. One gear has 4 teeth, and the other has 6 teeth. The LCM of 4 and 6 will tell you how many teeth each gear needs to rotate before they are both back in their starting positions simultaneously. This concept extends to more complex scenarios like scheduling tasks, planning events, and even understanding musical harmonies. The LCM helps us find the point at which different cycles align, making it an essential tool in various fields.
Comprehensive Overview of Least Common Multiple (LCM)
To fully grasp the concept of LCM, it's essential to understand its definition, how it relates to the greatest common divisor (GCD), and the various methods for calculating it. Let's explore these aspects in detail:
Definition of LCM
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In mathematical notation, it is often denoted as LCM(a, b) for two numbers a and b, and LCM(a, b, c) for three numbers a, b, and c, and so on.
Relationship with Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest positive integer that divides two or more integers without leaving a remainder. The LCM and GCD are related by the following formula:
LCM(a, b) = (|a| * |b|) / GCD(a, b)
This formula provides a way to calculate the LCM if you know the GCD, and vice versa. The GCD helps in simplifying fractions and finding common denominators, while the LCM is used for finding common multiples.
Methods to Calculate LCM
There are several methods to calculate the LCM of two or more numbers. The most common methods include:
-
Listing Multiples:
- List the multiples of each number.
- Identify the smallest multiple that is common to all the lists.
- This common multiple is the LCM.
-
Prime Factorization:
- Find the prime factorization of each number.
- Identify the highest power of each prime factor that appears in any of the factorizations.
- Multiply these highest powers together to get the LCM.
-
Division Method:
- Divide the numbers by their common prime factors.
- Continue dividing until no common prime factors remain.
- Multiply all the divisors and the remaining numbers to get the LCM.
Calculating LCM of 4 and 6
Let's apply these methods to find the LCM of 4 and 6:
-
Listing Multiples:
- Multiples of 4: 4, 8, 12, 16, 20, 24, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, ...
- The smallest common multiple is 12.
-
Prime Factorization:
- Prime factorization of 4: 2^2
- Prime factorization of 6: 2 * 3
- The highest power of 2 is 2^2, and the highest power of 3 is 3^1.
- LCM(4, 6) = 2^2 * 3 = 4 * 3 = 12
-
Division Method:
- Divide 4 and 6 by their common prime factor, 2:
- 4 / 2 = 2
- 6 / 2 = 3
- Since 2 and 3 have no common factors, multiply all the divisors and remaining numbers:
- LCM(4, 6) = 2 * 2 * 3 = 12
- Divide 4 and 6 by their common prime factor, 2:
Why is LCM Important?
The least common multiple (LCM) is not just a theoretical concept; it has practical applications in various fields. Understanding and being able to calculate the LCM is useful in:
- Mathematics: Simplifying fractions, solving equations, and understanding number theory.
- Scheduling: Coordinating events with different cycles or frequencies.
- Engineering: Designing gears, synchronizing machines, and optimizing processes.
- Music: Understanding harmonies and rhythms.
- Everyday Life: Planning activities, managing time, and solving problems involving repetitive cycles.
Trends and Latest Developments
In recent years, the concept of least common multiple (LCM) has seen advancements in computational methods and applications. Here are some trends and developments:
Computational Advancements
With the rise of computer science and algorithms, efficient methods for calculating the LCM of large numbers have been developed. These algorithms often use the relationship between LCM and GCD to optimize the computation, making it faster and more accurate. For very large numbers, specialized algorithms like the Euclidean algorithm for finding the GCD are employed to enhance performance.
Educational Tools
Interactive software and online calculators have made learning about LCM more accessible. These tools often provide step-by-step solutions and visual representations, helping students grasp the concept more effectively. Educational games and apps also incorporate LCM problems to make learning fun and engaging.
Real-World Applications
The applications of LCM continue to expand as technology advances. In computer science, LCM is used in scheduling tasks in operating systems and managing memory allocation. In cryptography, LCM is employed in certain encryption algorithms. In logistics and supply chain management, LCM helps optimize delivery schedules and coordinate transportation routes.
Professional Insights
From a professional perspective, understanding LCM can lead to more efficient problem-solving in various industries. For example, in project management, knowing the LCM of task durations can help in creating realistic timelines and avoiding conflicts. In finance, LCM can be used to analyze investment cycles and plan financial strategies. By mastering the concept of LCM, professionals can enhance their analytical skills and make more informed decisions.
Tips and Expert Advice
To truly master the concept of the least common multiple (LCM), here are some practical tips and expert advice:
Practice Regularly
Like any mathematical concept, practice is key to mastering the LCM. Solve a variety of problems with different numbers to reinforce your understanding. Start with simple examples and gradually move to more complex problems. Regular practice will help you become more confident and efficient in calculating the LCM.
Understand the Underlying Principles
Don't just memorize the formulas; understand why they work. Knowing the underlying principles will help you apply the concept of LCM in different contexts and solve problems more creatively. For example, understanding the relationship between LCM and GCD can provide a deeper insight into number theory and its applications.
Use Visual Aids
Visual aids like diagrams and charts can help you visualize the multiples and common multiples of numbers. This can be particularly useful for students who are visual learners. Creating a visual representation of the LCM can make the concept more intuitive and easier to remember.
Apply LCM to Real-World Problems
Look for opportunities to apply the concept of LCM to real-world problems. This will not only reinforce your understanding but also demonstrate the practical relevance of the concept. For example, try to calculate the LCM of different event schedules or task durations in your daily life.
Seek Help When Needed
Don't hesitate to ask for help if you're struggling with the concept of LCM. Consult your teacher, classmates, or online resources for clarification. There are many tutorials, videos, and interactive tools available that can help you understand the LCM better.
Utilize Prime Factorization
Prime factorization is a powerful tool for calculating the LCM, especially for larger numbers. Mastering prime factorization will not only help you find the LCM but also enhance your understanding of number theory. Practice factoring numbers into their prime components and use this skill to calculate the LCM efficiently.
Check Your Answers
Always check your answers to ensure accuracy. You can verify your answer by dividing the LCM by each of the given numbers to see if the result is an integer. This will help you catch any errors and reinforce your understanding of the concept.
Explore Advanced Topics
Once you have a good grasp of the basic concept of LCM, explore advanced topics such as the LCM of algebraic expressions or the LCM of more than two numbers. This will challenge you to think critically and apply your knowledge in new and different ways.
Use Technology Wisely
While technology can be a valuable tool for calculating the LCM, it's important to use it wisely. Don't rely solely on calculators or software; make sure you understand the underlying principles and can solve problems manually. Technology should be used as a tool to enhance your understanding, not replace it.
FAQ About Least Common Multiple (LCM)
Q: What is the difference between LCM and GCD? A: The least common multiple (LCM) is the smallest multiple that two or more numbers have in common, while the greatest common divisor (GCD) is the largest factor that two or more numbers have in common.
Q: How do I find the LCM of more than two numbers? A: You can find the LCM of more than two numbers by using the prime factorization method or the division method. Simply find the LCM of the first two numbers, and then find the LCM of that result with the next number, and so on.
Q: Is the LCM always larger than the given numbers? A: No, the LCM can be equal to one of the given numbers if that number is a multiple of all the other numbers. For example, the LCM of 2, 4, and 8 is 8.
Q: Can the LCM be zero? A: No, the LCM is always a positive integer. Zero is a multiple of every number, but it is not considered the least common multiple.
Q: What are some real-world applications of LCM? A: LCM is used in scheduling, engineering, music, and everyday problem-solving. It helps coordinate events, design gears, understand harmonies, and solve problems involving repetitive cycles.
Conclusion
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications. Understanding how to find the LCM of numbers like 4 and 6 is not only essential for academic success but also valuable for solving real-world problems. By mastering the methods for calculating LCM and understanding its relationship with other mathematical concepts, you can enhance your problem-solving skills and analytical abilities. Whether you're a student, engineer, musician, or just someone looking to simplify everyday calculations, the LCM is a powerful tool that can help you make sense of the world around you.
Now that you have a solid understanding of the least common multiple (LCM), put your knowledge to the test. Try solving some LCM problems on your own, explore advanced topics, and apply the concept to real-world scenarios. Share your insights and experiences with others, and help them discover the power of the LCM. Happy calculating!
Latest Posts
Latest Posts
-
How Many Days Until Feb 13
Nov 20, 2025
-
What Is The Square Root Of 121
Nov 20, 2025
-
Describing Words That Start With E
Nov 20, 2025
-
How Many Feet Is 60 Metres
Nov 20, 2025
-
How Many Cubic Feet Of Water Are In A Gallon
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.